cho đường tròn tâm o bán kính AB vẽ dây CD vuông góc với AB tại H (H nằm giữa O Và B) tia CD lấy E nằm ngoài đt EB cắt O tại F AF cắt DC tại K a) BFKH là tứ giác nội tiếp b) AB.BH=EB.BF
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 1 2022
a) Xét (O): E \(\in\) (O) (gt).
\(\Rightarrow\) \(\widehat{AEB}=90^o\) (Góc nội tiếp).
Xét tứ giác BEFI:
\(\widehat{AEB}+\widehat{CIB}=90^o+90^o=180^o.\)
Mà 2 góc này ở vị trí đối nhau.
\(\Rightarrow\) BEFI là tứ giác nội tiếp đường tròn.
b) Xét (O): \(CD\perp AB\) tại I (gt).
AB là đường kính; CD là dây (gt).
\(\Rightarrow\) I là trung điểm của CD.
Xét tam giác ACD:
AI là đường trung tuyến (I là trung điểm của CD).
AI là đường cao \(\left(AI\perp CD\right).\)
\(\Rightarrow\) Tam giác ACD cân tại A. \(\Rightarrow\) AC = AD (Tính chất tam giác cân).
Xét (O): AC = AD (cmt). \(\Rightarrow sđ\stackrel\frown{AC}=sđ\stackrel\frown{AD}.\)
Xét (O): \(\widehat{ACF}=\dfrac{1}{2}sđ\stackrel\frown{AD}\) (Góc nội tiếp).
Mà \(sđ\stackrel\frown{AD}=sđ\stackrel\frown{AC}\left(cmt\right).\)
\(\Rightarrow\) \(\widehat{ACF}=\dfrac{1}{2}sđ\stackrel\frown{AC}.\)
Mà \(\widehat{AEC}=\dfrac{1}{2}sđ\stackrel\frown{AC}\) (Góc nội tiếp).
\(\Rightarrow\widehat{ACF}=\widehat{AEC}.\)
Xét tam giác ACF và tam giác AEC:
\(\widehat{A}chung.\)
\(\widehat{ACF}=\widehat{AEC}\left(cmt\right).\)
\(\Rightarrow\) Tam giác ACF \(\sim\) Tam giác AEC (g - g).
\(\Rightarrow\) \(\dfrac{AC}{AE}=\dfrac{AF}{AC}\) (2 cạnh tương ứng tỉ lệ).
\(\Rightarrow AC^2=AE.AF\left(đpcm\right).\)
CM
14 tháng 7 2017
a, Học sinh tự chứng minh
b, DADB vuông tại D, có đường cao DH Þ A D 2 = AH.AB
c, E A C ^ = E D C ^ = 1 2 s đ E C ⏜ ; E A C ^ = K H C ^ (Tứ giác AKCH nội tiếp)
=> E D C ^ = K H C ^ => DF//HK (H là trung điểm DC nên K là trung điểm FC) => Đpcm
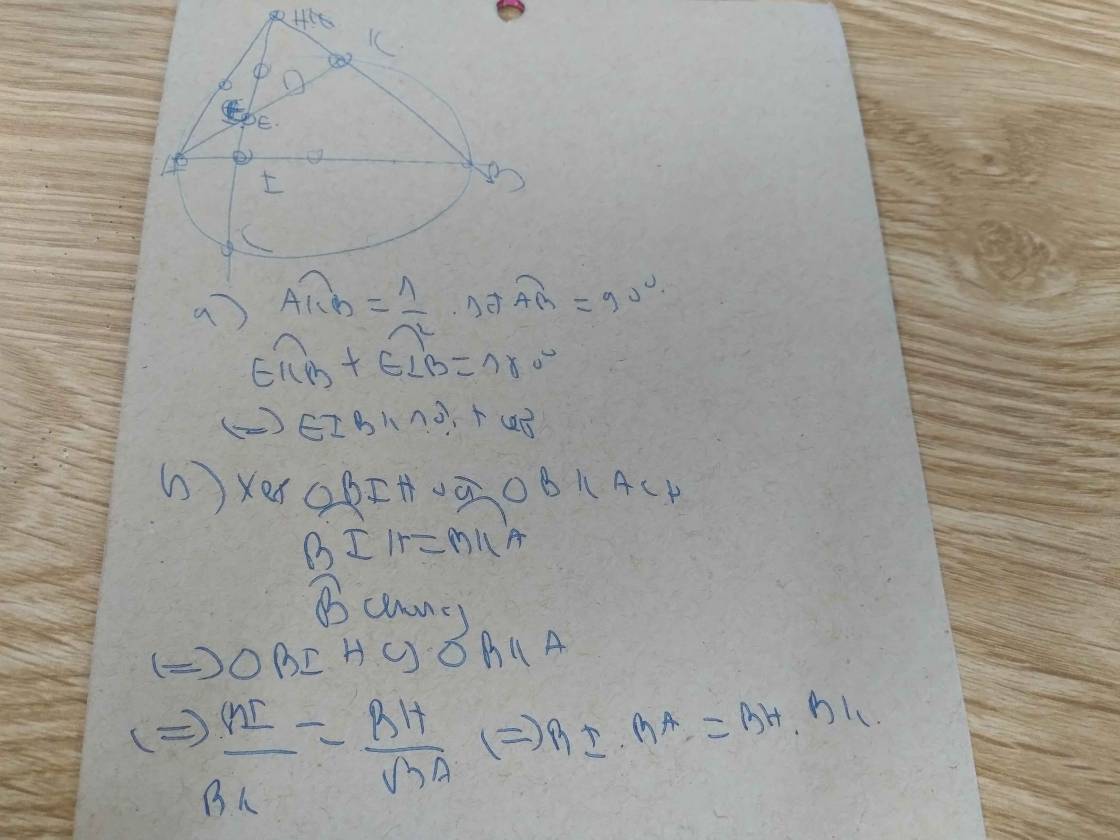
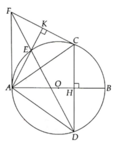
a: góc AFB=1/2*sđ cung AB=90 độ
góc KHB+góc KFB=90 độ
=>BHKF nội tiếp
b: Xét ΔBHE vuông tại H và ΔBFA vuông tại F có
goc B chung
=>ΔBHE đồng dạng với ΔBFA
=>BH/BF=BE/BA
=>BH*BA=BF*BE