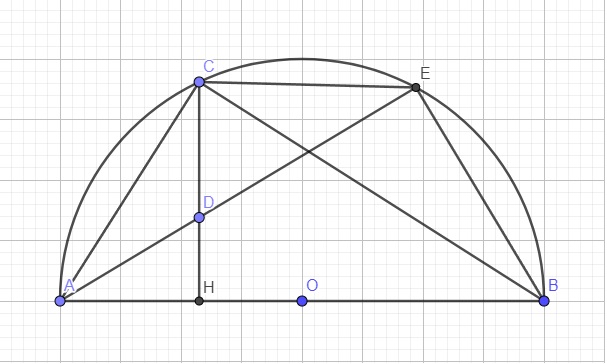
Cho nữa đường tròn (O) đường kính AB = 2R và điểm C nằm trên nữa đường tròn đó. Kẻ CH vuông góc với AB (H khác O). gọi D là điểm bất kì nằm trên đoạn CD, đường thẳng AD cắt nửa đường tròn tại điểm thứ hai là E
a, CM tứ giácBHDE nội tiếp
b, CM AD.EC=CD.AC
c, khi điểm C di động trên nửa đường tròn (C khác A, B và điểm chính giữa cung AB) , xác định vị trí của điểm C sao cho chu vi △COH đạt gía trị lớn nhất




a: góc AEB=1/2*sđ cung AB=90 độ
Vì góc DHB+góc DEB=180 độ
nên DHBE nội tiếp
b: Xét ΔADC và ΔACE co
góc ACH=góc AEC(=góc ABC)
góc DAC chung
=>ΔADC đồng dạng với ΔACE
=>DC/EC=AD/AC
=>DC*AC=EC*AD