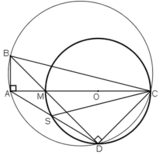
Cho tam giác ABC vuông tạo A, Trên cạnh AC lấy điểm M sao cho AC=3AM. Vẽ đường tròn tâm O, đường kính MC, cắt BC tại E, cắt tia BM tại D
a)Chứng minh tứ giác ABCD nội tiếp
b)Chứng minh góc BAE bằng góc BCD
c)Chứng minh rằng AB,CD và EM đồng qui
Giải giúp mình với ạ, chân thành cảm ơn!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 11 2019
a)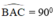 
⇒ A ∈ đường tròn đường kính BC.
D ∈ đường tròn đường kính MC
⇒ D ∈ đường tròn đường kính BC
⇒ A, B, C, D cùng thuộc đường tròn đường kính BC
hay tứ giác ABCD nội tiếp.
b) Xét đường tròn đường kính BC:
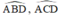đều là góc nội tiếp chắn cung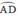 
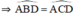
c) + Trong đường tròn đường kính MC:
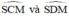đều là các góc nội tiếp cùng chắn cung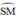 
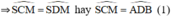
+ Trong đường tròn đường kính BC:
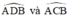đều là các góc nội tiếp chắn cung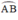 
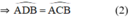
AH
Akai Haruma
Giáo viên
12 tháng 7 2021
Lời giải:
1.
$\widehat{MDC}=90^0$ (góc nt chắn nửa đường tròn)
$\Leftrightarrow \widehat{BDC}=90^0$
Tứ giác $ABCD$ có $\widehat{BAC}=\widehat{BDC}=90^0$ và cùng nhìn cạnh $BC$ nên là tgnt.
Do $ABCD$ nội tiếp nên $\widehat{BCA}=\widehat{BDA}$
Mà $\widehat{BDA}=\widehat{MCS}$ (do $MDSC$ nội tiếp)
$\Rightarrow \widehat{BCA}=\widehat{MCS}$
$\Rightarrow CA$ là phân giác $\widehat{BCS}$
2.
Gọi $T$ là giao điểm của $BA$ và $EM$
Xét tam giác $BTC$ có $TE\perp BC$ (do $\widehat{MEC}=90^0$) và $CA\perp BT$ và $TE, CA$ giao nhau tại $M$ nên $M$ là trực tâm tam giác $BTC$
$\Rightarrow BM\perp TC$.
Mà $BM\perp DC$ nên $TC\parallel DC$ hay $T,D,C$ thẳng hàng
Do đó $BA, EM, DC$ đồng quy tại $T$
3.
Vì $ABCD$ nt nên $\widehat{MAD}=\widehat{CAD}=\widehat{DBC}=\widehat{MBE}$
Dễ cm $BAME$ nội tiếp cho $\widehat{A}+\widehat{E}=90^0+90^0=180^0$ nên $\widehat{MBE}=\widehat{EAM}$
Do đó: $\widehat{MAD}=\widehat{EAM}$ nên $AM$ là tia phân giác $\widehat{EAM}(*)$
Mặt khác:
Cũng do $MECD,ABCD$ nội tiếp nên:
$\widehat{ADM}=\widehat{ADB}=\widehat{ACB}=\widehat{MCE}=\widehat{MDE}$
$\Rightarrow DM$ là tia phân giác $\widehat{ADE}(**)$
Từ $(*); (**)\Rightarrow M$ là tâm đường tròn nội tiếp $ADE$.
a: góc CDM=1/2*sđ cung CM=90 độ
góc CAB=góc CDB=90 độ
=>ABCD nội tiếp
c: Gọi F là giao của AB và CD
góc MEC=1/2*sđ cung MC=90 độ
=>ME vuông góc CB(1)
Xet ΔFCB có
CA,BD là đường cao
CA cắt BD tại M
=>M là trực tâm
=>FM vuông góc BC(2)
Từ (1), (2) suy ra F,M,E thẳng hàng