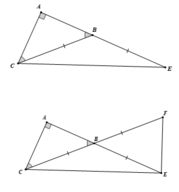
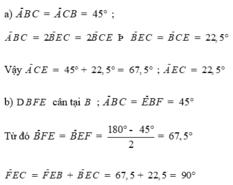Cho \(\Delta ABC\)vuông tại A. Vẽ về phía ngoài tam giác ABC các tam giác đều ABD và ACE. Gọi I là giao điểm của BE và CD. Chứng minh rằng \(\widehat{EIC}=60^0\)và IA là tia phân giác của \(\widehat{DIE}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 3 2020
Bạn tham khảo, có cả hình vẽ và bài làm nữa nhé: https://h7.net/hoi-dap/toan-7/chung-minh-tam-giac-bde-can-biet-cac-tam-giac-deu-abd-va-ace-faq380037.html
16 tháng 1 2020
a) +) Chứng minh \(\Delta\)DAC = \(\Delta\)BAE
Thật vậy: Ta có: AD = AB ( \(\Delta\)DAB đều )
^DAB = ^CAE ( = 60\(^o\); \(\Delta\)DAB đều ; \(\Delta\)CAE đều ) => ^DAC = ^BAE
CA = AE ( \(\Delta\)CAE đều )
Từ 3 điều trên => \(\Delta\)DAC = \(\Delta\)BAE ( c.g.c) (1)
=> ^ABE = ^ADC (2)
+) Xét \(\Delta\)KAD và \(\Delta\)KIB có: ^DKA = ^BKI ( đối đỉnh )
^KDA = ^KBI( theo ( 2) )
mà ^DKA + ^KDA + ^KAD= ^BKI + ^KBI + ^KIB = 180\(^o\)
=> ^KIB = ^KAD = ^BAD= 60\(^o\)
=> ^DIB = 60\(^o\)
b) Từ (1) => DC = BE mà M là trung điểm DC; N là trung điểm BE
=> DM = BN (3)
+) Xét \(\Delta\)BAN và \(\Delta\)DAM
có: BN = DM ( theo (3)
^ABN = ^ADM ( theo (2)
AB = AD ( \(\Delta\)ADB đều )
=> \(\Delta\)BAN = \(\Delta\)DAM (4)
=> AN = AM => \(\Delta\)AMN cân tại A (5)
+) Từ (4) => ^BAN = ^DAM => ^BAM + ^MAN = ^DAB + ^BAM
=> ^MAN = ^DAB = 60\(^o\)(6)
Từ (5); (6) => \(\Delta\)AMN đều
c) +) Trên tia đối tia MI lấy điểm F sao cho FI = IB => \(\Delta\)FIB cân tại I
mà ^BIF = ^BID = 60\(^{\text{}o}\)( theo (a))
=> \(\Delta\)FIB đều (7)
=> ^DBA = ^FBI( =60\(^o\))
=> ^DBF + ^FBA = ^FBA + ^ABI
=> ^DBF = ^ABI
Lại có: BI = BF ( theo (7) ) và BA = BD ( \(\Delta\)BAD đều )
Từ (3) điều trên => \(\Delta\)DFB = \(\Delta\)AIB => ^AIB = ^DFB = 180\(\text{}^o\)- ^BFI = 180\(\text{}^o\)-60\(\text{}^o\)=120\(\text{}^o\)
+) Mặt khác ^BID = 60 \(\text{}^o\)( theo (a) )
=> ^DIE = 180\(\text{}^o\)- ^BID = 120 \(\text{}^o\)và ^DIA = ^AIB - ^BID = 120\(\text{}^o\)-60\(\text{}^o\)=60\(\text{}^o\)
=> ^AIE = ^DIE - ^DIA = 120\(\text{}^o\)-60\(\text{}^o\)=60\(\text{}^o\)
=> ^DIA = ^AIE ( = 60\(\text{}^o\))
=> IA là phân giác ^DIE.
27 tháng 3 2019
Xét \(\Delta DAC\)và \(\Delta BAE\) có:\(DA=BA;\widehat{DAC}=\widehat{EAB}\left(=60^0+\widehat{BAC}\right);AC=AE\Rightarrow\Delta DAC=\Delta BAE\left(c.g.c\right)\Rightarrow\widehat{DCA}=\widehat{AEB}\)
Ta có:
\(\widehat{BIC}=\widehat{IEC}+\widehat{ECI}=\widehat{IEC}+\left(\widehat{ICA}+\widehat{ACE}\right)=\left(\widehat{IEC}+\widehat{AEI}\right)+\widehat{ACE}=\widehat{AEC}+\widehat{ACE}=60^0+60^0=120^0\)(Vì \(\widehat{AEB}=\widehat{ACI}\))
\(\Rightarrow\widehat{KIB}=60^0\Rightarrow\Delta KIB\)là tam giác đều \(\Rightarrow\widehat{KBI}=\widehat{BKI}=\widehat{BIK}=60^0;KB=IB\).
Ta có:\(\widehat{KBD}=\widehat{ABD}-\widehat{ABK}=60^0-\widehat{ABK}=\widehat{KBI}-\widehat{KBA}=\widehat{ABI}\)
Xét \(\Delta DKB\) và \(\Delta AIB\) có: \(DB=AB;\widehat{DBK}=\widehat{ABI}\left(cmt\right);KB=IB\Rightarrow\Delta DKB=\Delta AIB\left(c.g.c\right)\)
\(\Rightarrow\widehat{BIA}=\widehat{DKB}=180^0-60^0=120^0\)
\(\Rightarrow\widehat{AIE}=\widehat{AID}=120^0-60^0=60^0\) hay IA là phân giác \(\widehat{DIE}\).
26 tháng 3 2019
Sai đề rồi bạn.D,E phải nằm ở nửa mặt phẳng nào chứ???
