cho biểu thức M(x)=x2-x-2
tìm x nguyên để M(x) có giá trị là số nguyên tố
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
D
0
AH
Akai Haruma
Giáo viên
23 tháng 2 2022
Lời giải:
a. Để A là số nguyên tố thì 1 trong 2 thừa số $x-2, x+4$ có giá trị bằng 1 và số còn lại là số nguyên tố.
Mà $x-2< x+4$ nên $x-2=1$
$\Rightarrow x=3$
Thay vào $A$ thì $A=7$ là snt (thỏa mãn)
b. Để $A<0\Leftrightarrow (x-2)(x+4)<0$
Điều này xảy ra khi $x-2,x+4$ trái dấu. Mà $x-2< x+4$ nên:
$x-2<0< x+4$
$\Rightarrow -4< x< 2$
$x$ nguyên nên $x=-3,-2,-1,0,1$
CM
21 tháng 11 2017
Chọn đáp án B
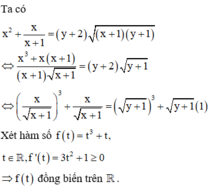
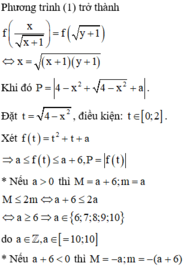
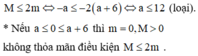
Vậy có 5 giá trị nguyên của m thỏa mãn điều kiện.
4 tháng 4 2023
Δ=(m+2)^2-4(m^2-1)
=m^2+4m+4-4m^2+4
=-3m^2+4m+8
Để phương trình có hai nghiệm thì -3m^2+4m+8>=0
=>\(\dfrac{2-2\sqrt{7}}{3}< =m< =\dfrac{2+2\sqrt{7}}{3}\)
x1-x2=2
=>(x1-x2)^2=4
=>(x1+x2)^2-4x1x2=4
=>(m+2)^2-4(m^2-1)=4
=>-3m^2+4m+8=4
=>-3m^2+4m+4=0
=>m=2 hoặc m=-2/3
17 tháng 3 2020
a) \(M=\frac{x}{x+1}+\frac{1}{x-1}-\frac{2x}{1-x^2}\left(x\ne\pm1\right)\)
\(\Leftrightarrow M=\frac{x}{x+1}+\frac{1}{x-1}+\frac{2x}{\left(x-1\right)\left(x+1\right)}\)
\(\Leftrightarrow M=\frac{x^2-x}{\left(x-1\right)\left(x+1\right)}+\frac{x+1}{\left(x-1\right)\left(x+1\right)}+\frac{2x}{\left(x-1\right)\left(x+1\right)}\)
\(\Leftrightarrow M=\frac{x^2-x+x+1+2x}{\left(x-1\right)\left(x+1\right)}\)
\(\Leftrightarrow M=\frac{x^2+2x+1}{\left(x-1\right)\left(x+1\right)}=\frac{\left(x+1\right)^2}{\left(x-1\right)\left(x+1\right)}=\frac{x+1}{x-1}\)
Vậy \(M=\frac{x+1}{x-1}\left(x\ne\pm1\right)\)
b) \(M=\frac{x+1}{x-1}\left(x\ne\pm1\right)\)
x-2=1
<=> x=3 (tmđk)
Thay x=3 vào M ta có: \(M=\frac{3+1}{3-1}=\frac{4}{2}=2\)
Vậy M=2 khi x-2=1
c) \(M=\frac{x+1}{x-1}\left(x\ne\pm1\right)\)
M nguyên khi x+1 chia hết cho x-1
=> x-1+2 chia hết cho x-1
x nguyên => x-1 nguyên => x-1 thuộc Ư (2)={-2;-1;1;2}
Ta có bảng
| x-1 | -2 | -1 | 1 | 2 |
| x | -1 | 0 | 2 | 3 |
| ĐCĐK | ktm | tm | tm | tm |
Vậy x={0;2;3}
NP
0
