Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) PTHH: \(CH_4+2O_2\underrightarrow{t^o}CO_2+2H_2O\)
\(C_2H_4+3O_2\underrightarrow{t^o}2CO_2+2H_2O\)
b) Đặt \(n_{CH_4}=x\left(mol\right);n_{C_2H_4}=y\left(mol\right)\). Khi đó \(22,4x+22,4y=4,48\) \(\Leftrightarrow x+y=0,2\)
Từ PTHH \(\Rightarrow n_{O_2\left(1\right)}=2x\left(mol\right)\)\(;n_{O_2\left(2\right)}=3y\left(mol\right)\). Khi đó \(2x.22,4+3y.22,4=11,2\) \(\Leftrightarrow2x+3y=0,5\)
Vậy ta có \(\left\{{}\begin{matrix}x+y=0,2\\2x+3y=0,5\end{matrix}\right.\Leftrightarrow x=y=0,1\left(mol\right)\)
\(\Rightarrow\%V_{CH_4}=\%V_{C_2H_4}=50\%\)
\(n_{CO_2}=\dfrac{5,6}{22,4}=0,25mol\)
\(\left\{{}\begin{matrix}CH_4:x\left(mol\right)\\C_2H_4:y\left(mol\right)\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}16x+28y=3,6\\BTC:x+2y=n_{CO_2}=0,25\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=0,05mol\\y=0,1mol\end{matrix}\right.\)
a)\(CH_4+2O_2\underrightarrow{t^o}CO_2+2H_2O\)
\(C_2H_4+3O_2\underrightarrow{t^o}2CO_2+2H_2O\)
b)\(m_{CH_4}=0,05\cdot16=0,8g\)
\(m_{C_2H_4}=0,1\cdot28=2,8g\)
c)\(\Sigma n_{O_2}=2n_{CH_4}+3n_{C_2H_4}=2\cdot0,05+3\cdot0,1=0,4mol\)
\(\Rightarrow V_{O_2}=0,4\cdot22,4=8,96l\)
\(\Rightarrow V_{kk}=5V_{O_2}=5\cdot8,96=44,8l\)
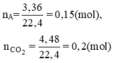
Gọi số mol của metan và etan lần lượt là x và y (mol)
Phương trình phản ứng:
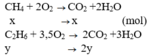
Vậy thành phần phần trăm về thể tích các khí trong hỗn hợp A là:
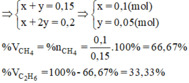
Câu 1:
\(a,PTHH:C_2H_4+5O_2\underrightarrow{t^o}2CO_2+2H_2O\)
\(n_{C_2H_4}=\dfrac{V_{\left(đktc\right)}}{22,4}=\dfrac{5,6}{22,4}=0,25\left(mol\right)\)
\(Theo.PTHH:n_{O_2}=5.n_{C_2H_4}=5.0,25=1,25\left(mol\right)\\ V_{O_2\left(đktc\right)}=n.22,4=1,25.22,4=28\left(l\right)\)
\(b,\Rightarrow V_{kk\left(đktc\right)}=5.V_{O_2\left(đktc\right)}=5.28=140\left(l\right)\)
B1:
\(C_2H_4+3O_2\rightarrow\left(t^o\right)2CO_2+2H_2O\)
Vì số mol tỉ lệ thuận với thể tích, đồng thời nhìn PTHH, ta sẽ được:
\(a,V_{O_2\left(đktc\right)}=3.V_{C_2H_4\left(đktc\right)}=3.5,6=16,8\left(l\right)\)
\(b,V_{kk}=5.V_{O_2\left(đktc\right)}=16,8.5=84\left(l\right)\)
B2:
Đặt số mol metan, etylen lần lượt là a,b (mol) (a,b>0)
\(n_{hh}=n_{CH_4}+n_{C_2H_4}=a+b=\dfrac{3,36}{22,4}=0,15\left(1\right)\)
PTHH: CH4 +2 O2 -to-> CO2 +2 H2O
C2H4 +3 O2 -to-> 2CO2 + 2H2O
\(n_{CO_2\left(tổng\right)}=a+2b=\dfrac{8,8}{44}=0,2\left(mol\right)\left(2\right)\)
(1), (2) =>a=0,1; b=0,05
Số mol tỉ lệ tương ứng với thể tích. Nên:
\(\%V_{CH_4}=\%n_{CH_4}=\dfrac{0,1}{0,15}.100\approx66,667\%\\ \Rightarrow\%V_{C_2H_4}\approx33,333\%\)
a, \(CH_4+2O_2\underrightarrow{^{t^o}}CO_2+2H_2O\)
\(C_2H_4+3O_2\underrightarrow{^{t^o}}2CO_2+2H_2O\)
b, Gọi: \(\left\{{}\begin{matrix}n_{CH_4}=x\left(mol\right)\\n_{C_2H_4}=y\left(mol\right)\end{matrix}\right.\) \(\Rightarrow x+y=\dfrac{4,48}{22,4}=0,2\left(mol\right)\left(1\right)\)
Theo PT: \(n_{O_2}=2n_{CH_4}+3n_{C_2H_4}=2x+3y=\dfrac{15,68}{22,4}=0,7\left(mol\right)\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}x=-0,1\\y=0,3\end{matrix}\right.\)
Đến đây thì ra số mol âm, bạn xem lại đề nhé.
a)
$CH_4 + 2O_2 \xrightarrow{t^o} CO_2 + 2H_2O$
b) Theo PTHH : $V_{O_2} = 2V_{CH_4} = 11,2(lít)$
$n_{CH_4} = \dfrac{5,6}{22,4} = 0,25(mol)$
Theo PTHH : $n_{H_2O} = 2n_{CH_4} = 0,5(mol)$
$m_{H_2O} = 0,5.18 = 9(gam)$
a, \(CH_4+2O_2\underrightarrow{t^o}CO_2+2H_2O\)
\(C_2H_4+3O_2\underrightarrow{t^o}2CO_2+2H_2O\)
b, Gọi: \(\left\{{}\begin{matrix}n_{CH_4}=x\left(mol\right)\\n_{C_2H_4}=y\left(mol\right)\end{matrix}\right.\) \(\Rightarrow x+y=\dfrac{4,48}{22,4}=0,2\left(mol\right)\left(1\right)\)
\(n_{CO_2}=n_{CH_4}+2n_{C_2H_4}=x+2y=\dfrac{5,6}{22,4}=0,25\left(mol\right)\left(2\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x=0,15\left(mol\right)\\y=0,05\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\%V_{CH_4}=\dfrac{0,15.22,4}{4,48}.100\%=75\%\\\%V_{C_2H_4}=100-75=25\%\end{matrix}\right.\)