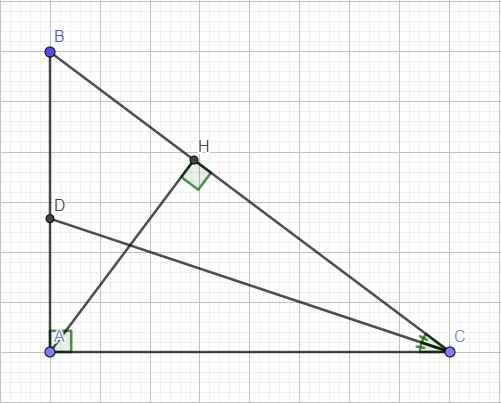
cho tam giác ABC vuông tại A có AB= 6cm và BC= 10cm.kẻ đường phan giác CD của tam giác ABC (D ϵ AB)
a) tính độ dài cạnh AC. Tính độ dài đoạn thẳng BD và AD.
b) kẻ đường cao AH (H ϵ BC). Chứng minh AB2=HB.BC. Từ đó suy ra độ dài AH.
c) AH cắt CD tại E. Chứng minh AD.EH=ED.BD