\(\text{Tìm số nguyên n để phân số A=}\dfrac{12n-1}{4n-3}\text{có giá trị nhỏ nhất}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




a: Để A là phân số thì 3n+3<>0
hay n<>-1
b: Để A là số nguyên thì \(4n⋮n+1\)
\(\Leftrightarrow n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
hay \(n\in\left\{0;-2;1;-3;3;-5\right\}\)

a: Để A là phân số thì 3n+3<>0
=>n<>-1
b: \(A=\dfrac{12n}{3\left(n+1\right)}=\dfrac{4n}{n+1}\)
Để A là số nguyên thì 4n+4-4 chia hết cho n+1
=>\(n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(n\in\left\{0;-2;1;-3;3;-5\right\}\)

a) Để A là một phân số thì mẫu của \(A\ne0\) hay \(2n+3\ne0\)
\(\Leftrightarrow n\ne\dfrac{-3}{2}\)
b) Ta có : \(A=\dfrac{12n+1}{2n+3}\)
\(\Rightarrow A=\dfrac{12n+18-17}{2n+3}=\dfrac{12n+18}{2n+3}-\dfrac{17}{2n+3}\)
\(\Rightarrow A=\dfrac{6\left(2n+3\right)}{2n+3}-\dfrac{17}{2n+3}=6-\dfrac{17}{2n+3}\)
Để \(A\in Z\Leftrightarrow\dfrac{17}{2n+3}\in Z\)
\(\Leftrightarrow2n+3\in U\left(17\right)\)
mà \(U\left(17\right)=\left(1;-1;17;-17\right)\)
\(\Rightarrow n\in\left(-1;-2;7;-10\right)\)
Vậy \(A\in Z\Leftrightarrow n\in\left(-1;-2;7;-10\right)\)

a: A là phân số khi 3n+3<>0
=>n<>-1
b: \(A=\dfrac{12}{3\left(n+1\right)}=\dfrac{4}{n+1}\)
Để A nguyên thì \(n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(n\in\left\{0;-2;1;-3;3;-5\right\}\)

\(\frac{4n+1}{2n+3}=\frac{4n+6-5}{2n+3}=\frac{2\left(2n+3\right)-5}{2n+3}=2-\frac{5}{2n+3}\)
Để \(2-\frac{5}{2n+3}\) là số nguyên <=> \(\frac{5}{2n+3}\) là số nguyên
=> 2n + 3 thuộc Ư(5) = { - 5; - 1; 1; 5 }
=> 2n + 3 = { - 5; - 1; 1; 5 }
=> n = { - 4; - 2; - 1 ; 1 }
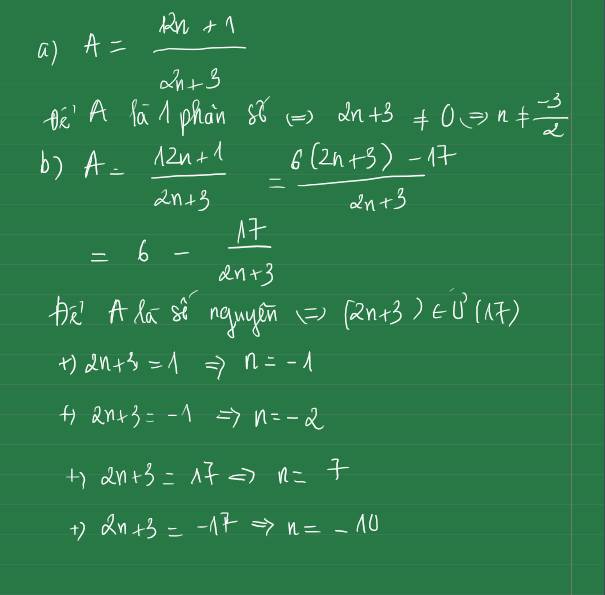
Ta có A=12n-1/4n+3=12n+9-10/4n+3=3.(4n+3)-10/4n+3=3-10/4n+3
Để A đạt giá trị nhỏ nhất thì 10/4n+3 đạt giá trị lớn nhất
+4n+3>0=>10/4n+3>0=>3-10/4n+3<3
+4n+3<0=>10/4n+3<0=>3-10/4n+3>3
Để A đạt giá trị nhỏ nhất thì 10/4n+3 đạt giá trị lớn nhất
=>4n+3 là số nguyên dương lớn nhất
=>4n+3
=>4n=-4
n=-4:4
n=-1
Khi đó A nhỏ nhất
Vậy A=-1
Chúc bạn học tốt cho mình điểm nhé