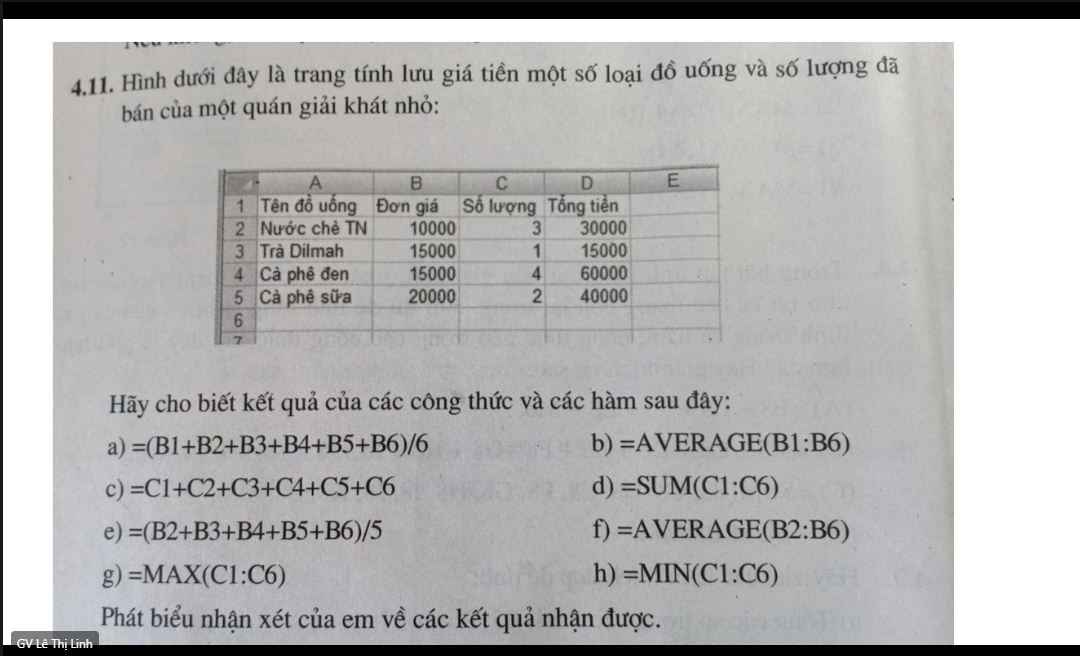
CHỈ MÌNH CÁCH LÀM BÀI NÀY VỚI Ạ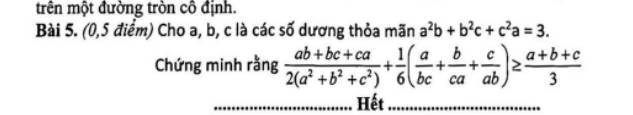
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Để làm dạng này , bạn làm như sau :
Vì bạn biết 1 giờ = 60 phút; 1 phút =60 giây nên là
Trước hết bạn lấy số 0,8325 (số chỉ giờ) nhân 60 nhé = 49,95
Bạn lấy phần nguyên của nó trước dấu phẩy là 49 , điền vảo chỗ chấm trước phút.
Cái phần thập phân sau dấu phẩy là 0,95 bạn tiếp tục nhân 60 = 57.
Bạn điền 57 vào phần chỗ chấm trước giây.
Vậy 0,8325 giờ=49 phút 57 giây

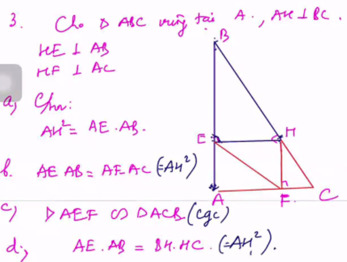
tất cả các ý mình cm thành cụm luôn nhé
Xét tam giác AHE và tam giác ABH ta có
^A _ chung
^AHE = ABH = 900
Vậy tam giác AHE ~ tam giác ABH (g.g)
\(\dfrac{AH}{AB}=\dfrac{AE}{AH}\Rightarrow AH^2=AE.AB\)(1)
Xét tam giác AHC và tam giác AFH có
^A _ chung
^AHC = ^AFH = 900
Vậy tam giác AHC ~ tam giác AFH (g.g)
\(\dfrac{AH}{AF}=\dfrac{AC}{AH}\Rightarrow AH^2=AF.AC\)(2)
Từ (1) ; (2) suy ra \(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)(*)
Xét tam giác AEF và tam giác ABC có
^A _ chung ; có (*)
Vậy tam giác AEF ~ tam giác ABC (c.g.c)

â) 4P +5 O2 -to-> 2 P2O5
b) nO2=5,6/22,4=0,25(mol)
=>nP=0,25 x 4/5 =0,2(mol)
=>mP=0,2.31=6,2(g)
c) nP=15,5/31=0,5(mol)
Ta có: 0,5/4 > 0,25/5
-> P dư, O2 hết, tính theo nO2.
=> nP2O5=2/5. 0,25=0,1(mol
=>mP2O5=142.0,1=14,2(g)

\(\dfrac{x+1}{2x^2-x^4}=\dfrac{x+1}{x^2\left(2-x^2\right)}=\dfrac{-\left(x+1\right)\left(x^4+2x^2+4\right)}{x^2\left(x^2-2\right)\left(x^4+2x^2+4\right)}\\ \dfrac{x}{x^4+2x^2+4}=\dfrac{x^3\left(x^2-2\right)}{x^2\left(x^2-2\right)\left(x^4+2x^2+4\right)}\\ \dfrac{2x-1}{x^7-8x}=\dfrac{2x-1}{x\left(x^6-8\right)}=\dfrac{x\left(2x-1\right)}{x^2\left(x^2-2\right)\left(x^4+2x^2+4\right)}\)

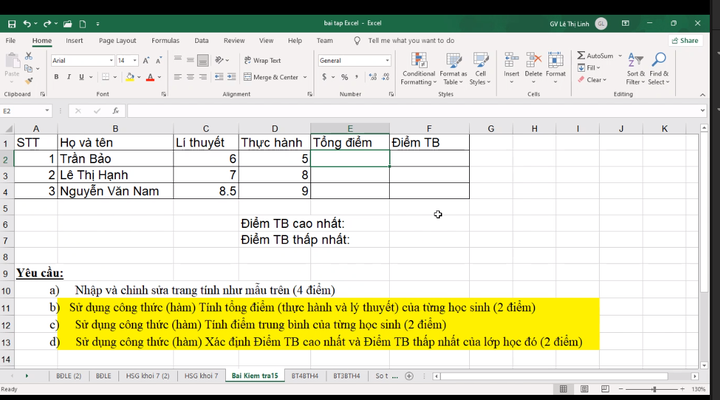
b) Nhập ở phần |Tổng Điểm|: =SUM(6;5) hay =SUM(C2;D2) Nhấn Enter=>Tổng điểm của Trần Bảo
=SUM(7;8) hay =SUM(C3;D3) Nhấn Enter=>Tổng điểm của Lê Thị Hạnh
=SUM((8,5;9) hay =SUM(C4;D4) Nhấn Enter=>Tổng điểm của Ng~ Văn Nam c) Nhập ở phần |Điểm TB|: =AVERAGE(6;5) hay =AVERAGE(C2;D2) Nhấn Enter=>ĐTB của Trần Bảo same
same
d) Phần này bạn dùng hàm MAX(cao nhất); MIN(thấp nhất) để tính dtb nhé( ở câu c)
Hình 2 mik lười làm quá thông cảm XD



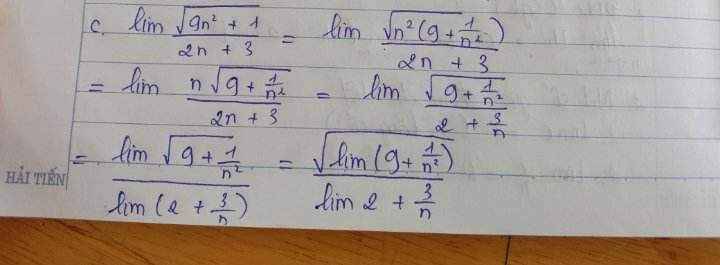





Ta có:
\(\dfrac{ab+bc+ca}{2\left(a^2+b^2+c^2\right)}+\dfrac{1}{6}\left(\dfrac{a^2+b^2+c^2}{abc}\right)\ge2\sqrt{\dfrac{1}{12}\left(\dfrac{ab+ca+ca}{abc}\right)}=\sqrt{3\left(\dfrac{ab+bc+ca}{abc}\right)}\)
Nên ta chỉ cần cm:
\(\sqrt{\dfrac{1}{3}\left(\dfrac{ab+bc+ca}{abc}\right)}\ge\dfrac{a+b+c}{3}\Leftrightarrow3\left(\dfrac{ab+bc+ca}{abc}\right)\ge\left(a+b+c\right)^2\)
Thật vậy, ta có:
\(\dfrac{3\left(ab+bc+ca\right)}{abc}=\dfrac{\left(a^2b+b^2c+c^2a\right)\left(ab+bc+ca\right)}{abc}\)
\(=\left(\dfrac{a}{c}+\dfrac{b}{a}+\dfrac{c}{b}\right)\left(ac+ab+bc\right)\ge\left(a+b+c\right)^2\) (Bunhiacopxki)
Dấu "=" xảy ra khi \(a=b=c=1\)