Ai cũng có thể dùng 12 que diêm xếp thành 3 hình vuông. Nhưng nếu chỉ có 10 que hay 11 que thì bạn có xếp được 3 hình vuông không ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 6 2017
A) Tổng độ dài của cả 11 que là:
1+2+3+4+5+6+7+8+9+10+11= 66 [ cm ]
Vì 66 không chia hết cho 4 nên không thể xếp thành một
hình vuông mà không thể bớt một mẩu que nào.
B) Nếu bớt một mẩu que thì có thể xếp thành hình vuông
những mẩu que có thể bớt là: 2, 6, 10
Cạnh của hình vuông khi bớt đi 2 cm:
[ 1+3+4+5+6+7+8+9+10+11 ] :4 = 16 [cm]
Cạnh của hình vuông khi bớt đi 6 cm:
[ 1+2+3+4+5+7+8+9+10+11 ] :4 = 15 [ cm ]
Cạnh của hình vuông khi bớt đi 10 cm:
[ 1+2+3+4+5+6+7+8+9+11 ] :4 = 9 [ cm ]
Đáp số : A) không thể
B) có thể
bớt 2 cm: 16 cm
bớt 6 cm: 15cm
bớt 10 cm: 9 cm
AK
8 tháng 7 2020
ĐKXĐ : \(1\ne x\ge0\)
Ta có : \(P=\frac{1}{\sqrt{x}-1}+\frac{\sqrt{x}}{x-1}=\frac{\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}+\frac{\sqrt{x}}{x-1}=\frac{\sqrt{x}+1+\sqrt{x}}{x-1}=\frac{2\sqrt{x}+1}{x-1}\)
\(Q=\left(\frac{\sqrt{x}}{\sqrt{x}-1}-1\right)=\frac{\sqrt{x}-\sqrt{x}+1}{\sqrt{x}-1}=\frac{1}{\sqrt{x}-1}\)
Suy ra : \(M=\frac{P}{Q}=\frac{2\sqrt{x}+1}{x-1}:\frac{1}{\sqrt{x}-1}=\frac{2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\left(\sqrt{x}-1\right)=\frac{2\sqrt{x}+1}{\sqrt{x}+1}\)
Vậy ...
CM
16 tháng 10 2018
Phương pháp giải:
Di chuyển hai trong số các que diêm, sao cho tạo với các que diêm còn lại 3 hình vuông.
Lời giải chi tiết:
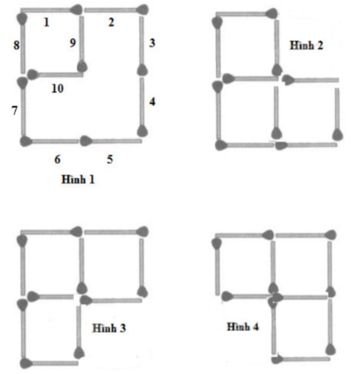
Ta gọi số thứ tự của các que diêm là 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 như hình 1.
- Ta di chuyển hai que diêm 2 và 3 xuống dưới thì được hình 2.
- Ta di chuyển hai que diêm 4 và 5 thì được hình 3.
- Ta di chuyển hai que diêm 7 và 6 thì được hình 4.
31 tháng 8 2016
Lấy que bên trái hình vuông thứ nhất ghép thành số ba. Bằng cách lấy thêm hai que diêm dư còn lại sẽ thành 3
D
4
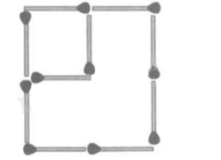
10 que diêm xếp thành 3 hình vuông
11 que diêm xếp thành 3 hình vuông
Cảm ơn bạn nhé!