Trong không gian cho đường thẳng Δ và điểm O. Qua O có mấy đường thẳng vuông góc với Δ cho trước?
A. 1
B. 2
C. 3
D. Vô số
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
- Qua điểm O có thể dựng vô số đường thẳng vuông góc với Δ, các đường thẳng đó cùng nằm trong một mặt phẳng vuông góc với Δ.

Đáp án B
- Phương pháp:
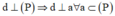
- Cách giải: Trong không gian cho đường thẳng Δ và điểm O. Qua O có vô số đường thẳng vuông góc Δ. Chúng nằm trong mặt phẳng qua O và vuông góc với Δ.

Chọn đáp án D.

Cách 2: Nhận thấy tọa độ điểm I không thỏa mãn phương trình ở phương án A và phương án C nên loại hai phương án này.
d có một vectơ chỉ phương là ![]()
Đường thẳng có phương trình trong phương án B có vectơ chỉ phương ![]()
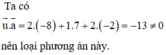

Đáp án C
Để tìm đường thẳng đã cho trước hết ta cần xác định mặt phẳng (P) đi qua A và vuông góc với d. Khi đó đường thẳng Δ cần tìm nằm trên (P).
Mặt cầu (S) có tâm I(1;2;0), bán kính R = 2 .
Đường thẳng d có véc tơ chỉ phương u → = 2 ; 1 ; 1 .
Gọi (P) là mặt phẳng đi qua A và vuông góc với d suy ra n P → = u → = 2 ; 1 ; 1 .
Phương trình mặt phẳng P : 2 x − 1 + y + z = 0 ⇔ P : 2 x + y + z − 2 = 0 .
Giả sử tiếp điểm Δ và mặt cầu (S) là điểm M(x;y;z)

Vậy có hai tiếp tuyến thỏa mãn yêu cầu bài toán là
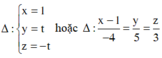
Chọn A