Cho hai số có tích bằng 99; nếu tăng số thứ hai lên 5 đơn vị thì tích mới bằng 144. Tìm hai số đó?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DD
Đoàn Đức Hà
Giáo viên
9 tháng 3 2022
Sau khi bớt cùng một số k ở cả hai số thì hiệu hai số không đổi.
Hiệu hai số là:
\(99-67=32\)
Nếu hai số mới có số thứ nhất là \(3\)phần thì số thứ hai là \(5\)phần.
Hiệu số phần bằng nhau là:
\(5-3=2\)(phần)
Số thứ nhất mới là:
\(32\div2\times3=48\)
Số k là:
\(67-48=19\)
CM
18 tháng 4 2018
Gọi chữ số hàng chục là x, chữ số hàng đơn vị là y.
Điều kiện x ∈N* và x ≤ 9; y ∈N* và y ≤ 9.
Số có hai chữ số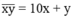 
và số đổi chỗ:
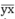= 10y + x
Đổi chỗ hai chữ số thì được một số lớn hơn số đã cho là 63, ta có:
(10y + x) – (10x + y) = 63
Tổng của số đã cho và số mới tạo thành bằng 99, ta có:
(10x + y) + (10y + x) = 99
Ta có hệ phương trình:
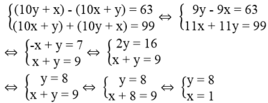
Ta thấy x = 1, y = 8 thỏa điều kiện bài toán.
Vậy số cần tìm là 18.
DE
18 tháng 8 2019
Gọi chữ số hàng chục là x, chữ số hàng đơn vị là y.
Điều kiện: x ∈ N* và x ≤ 9; y ∈ N* và y ≤ 9
Số đã cho xy=10x+y; số đổi chỗ yx=10y+x
Đổi chỗ hai chữ số ta được số mới lớn hơn số đã cho 63.
Ta có phương trình: (10y+x)–(10x+y)=63
Tổng của số mới và số đã cho bằng 99, ta có phương trình:
(10x+y)+(10y+x)=99
Ta có hệ phương trình:
(10y+x)–(10x+y)=63
(10x+y)+(10y+x)=99
⇔9y–9x=63
11x+11y=99
⇔–x+y=7
x+y=9
⇔2y=16
x+y=9
⇔y=8
x+8=9
⇔y=8
x=1
Với x =1; y = 8 thỏa mãn điều kiện bài toán
Vậy số đã cho là 18.
ND
0
5 đơn vị ứng với số phần là :
144-99=45
số thứ nhất là '
45 :5=9
số thứ hai là :
99 :9=11
vậy sô thứ nhất : 9
số thứ hai :11
Gọi số thứ nhất là A , số thứ hai là B
AxB= 99
Ax( B+5) = 144
AxB + Ax5 = 144
99+ Ax5 = 144
Ax5 = 144-99= 45
A= 45:5= 9
B = 99 : 9 =11