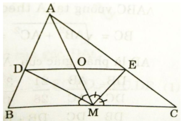
Cho ∆ABC có AM là trung tuyến, các đường phân giác của góc BMA và góc CMA cắt AB, AC lần lượt tại D và E.
a) Chứng minh DE//BC.
b) Gọi O là giao điểm của AM và DE. C/m: OD=OE.
Cíu đi =(
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
9 tháng 12 2019
a) DM là đường phân giác của ΔABM nên theo tính chất đường phân giác của tam giác ta có:
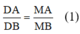
Tương tự EM là đường phân giác ΔACM nên:
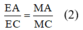
Mà MB = MC nên từ (1) và (2) suy ra
NH
28 tháng 4 2020
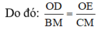
a, Vì MD là phân giác AMB \(\Rightarrow\frac{AD}{AM}=\frac{BD}{BM}\)\(\Rightarrow\frac{AD}{BD}=\frac{AM}{BM}\)\(\Rightarrow\frac{AD}{BD}=\frac{AM}{CM}\)(MB = MC)
Vì ME là phân giác AMC \(\Rightarrow\frac{AE}{AM}=\frac{EC}{MC}\)\(\Rightarrow\frac{AE}{EC}=\frac{AM}{MC}\)
\(\Rightarrow\frac{AE}{EC}=\frac{AD}{BD}\) => DE // BC (định lý Thales đảo)
b, Vì DE // BE (cmt) \(\Rightarrow\frac{DO}{BM}=\frac{AO}{OM}\)(Hệ quả định lý Thales) và \(\frac{OE}{MC}=\frac{OA}{OM}\) (Hệ quả định lý Thales)
\(\Rightarrow\frac{DO}{BM}=\frac{OE}{MC}\)
Mà BM = MC (gt)
=> DO = OE
23 tháng 4 2020
a) Vì AM là trung tuyến của \(\Delta ABC\Rightarrow BM=CM;M\in BC\)
Xét \(\Delta ABM\)có MD là p/g \(\widehat{BMA}\Rightarrow\frac{AD}{BD}=\frac{AM}{BM}\)hay \(\frac{AD}{BD}=\frac{AM}{CM}\left(1\right)\)
Xét \(\Delta ACM\)có ME là p/g \(\widehat{CMA}\Rightarrow\frac{AE}{CE}=\frac{AM}{CM}\left(2\right)\)
Từ (1)(2)\(\Rightarrow\frac{AD}{BD}=\frac{AE}{CE}\Rightarrow DE//BC\)(đ/ lí Ta-lét đảo)
b) Có \(DE//BC\), \(O\in DE,M\in BC\Rightarrow OD//BM;OE//CM\)
Xét \(\Delta ABM\)có \(OD//BM\Rightarrow\frac{OD}{BM}=\frac{OA}{AM}\left(3\right)\)
Xét \(\Delta ACM\)có \(OE//CM\Rightarrow\frac{OE}{CM}=\frac{OA}{AM}\left(4\right)\)
Từ (3)(4) \(\Rightarrow\frac{OD}{BM}=\frac{OE}{CM}\).Mà BM=CM \(\Rightarrow OD=OE\)
4 tháng 3 2023
a: Xét ΔMAB có MD là phân giác
nên AD/DB=AM/MB=AM/MC
Xét ΔAMC có ME là phân giác
nên AE/EC=AM/MC
=>AD/DB=AE/EC
=>ED//BC
b: Xét ΔABM có DI//BM
nên DI/BM=AI/AM
Xét ΔACM có EI//MC
nên EI/CM=AI/AM
=>DI/BM=EI/CM
=>DI=EI
19 tháng 2 2023
a: Xét ΔMAB có MD là phân giác
nên AD/DB=AM/MB=AM/MC
Xét ΔMAC ó ME là phân giác
nên AE/EC=AM/MC=AD/DB
=>ED//BC
b: Xét ΔMAB có MD là phân giác
nên AD/DB=AM/MB=5/3
=>AD/AB=5/8
Xét ΔABC có DE//BC
nên DE/BC=AD/AB
=>DE/6=5/8
=>DE=3,75cm
DT
Đỗ Thanh Hải
CTVVIP
27 tháng 2 2021
a) 
b) ta có MD là tia phân giác của \(\widehat{AMB}\), ME là tia phân giác của \(\widehat{AMC}\)
=> \(\widehat{AMD}=\widehat{DMB}=\dfrac{1}{2}\widehat{AMB}\) và \(\widehat{AME}=\widehat{EMC}=\dfrac{1}{2}\widehat{AMC}\)
=> \(\widehat{AME}+\widehat{AMD}=\dfrac{\widehat{AMC}+\widehat{AMB}}{2}=\dfrac{180^o}{2}=90^o\)
Ta có \(\widehat{EMC}=\widehat{MED}\)(do ED//BC)
mà \(\widehat{EMC}=\widehat{EMI}\)
=> \(\widehat{EMI}=\widehat{MEI}\)=> tam giác EIM cân tại I
=> EI=IM
cmtt : IM=ID
=> EI=IM=MD
=> IM = \(\dfrac{1}{2}\left(EI+ID\right)=\dfrac{1}{2}ED\)(ĐPCM)
a: Xét ΔMAB có MD là phan giác
nên MA/MB=AD/DB=MA/MC
Xét ΔMAC có ME là phân giác
nên MA/MC=AE/EC
=>AD/DB=AE/EC
=>DE//BC
b: Xét ΔAMB có OD//MB
nên OD/MB=AO/AM
Xét ΔAMC có OE//MC
nên OE/MC=AO/AM
=>OD/MB=OE/MC
mà MB=MC
nên OD=OE