cho đoạn thẳng ab trên cùng 1 nửa mặt phẳng có bờ là đường thẳng ab vẽ hai tia ax và by lần lượt vuông góc với ab tại a và b gọi trung điểm của ab là o trên ax lấy điểm c trên by lấy điểm d sao cho góc COD bằng 90 độ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
HM
Hữu Minh
17 tháng 2 2023
Đúng(0)
Những câu hỏi liên quan
TN
22 tháng 5 2018
Bạn tự vẽ hình nha
Câu a
Chứng minh : Kẻ OC cắt BD tại E
Xét ΔCAO và ΔEBO có :
ˆA=^OBE (=1v)
AO=BO (gt)
^COA=^BOE (đối đỉnh)
⇒ΔCAO=ΔEBO (cgv - gn )
⇒OC=OE ( hai cạnh tương ứng )
và AC=BE ( hai cạnh tương ứng )
Xét ΔOCD và ΔOED có :
OC=OE (c/m trên )
^COD=^DOE ( = 1v )
OD chung
⇒ΔOCD=ΔOED (cgv - cgv )
⇒CD=DE (hai cạnh tương ứng )
mà DE = BD + BE
và AC = BE ( c/m trên )
⇒CD=AC+BD
7 tháng 4 2020
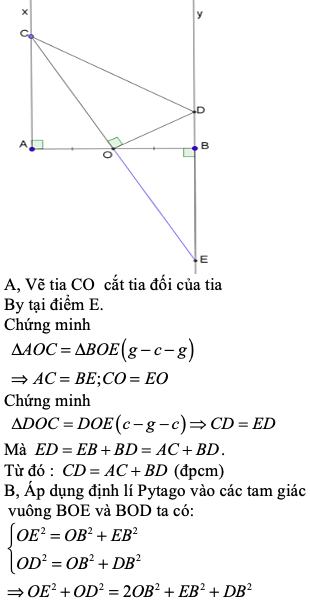
a) Vẽ tia CO cắt tia đối của tia By tại E
Xét tam giác vuông AOC và tam giác vuông BOE có :
AO = OB ( gt )
AOC = BOE ( 2 góc đối đỉnh )
\(\implies\) tam giác vuông AOC = tam giác vuông BOE ( cạnh huyền - góc nhọn )
\(\implies\) AC = BE ( 2 cạnh tương ứng )
Xét tam giác vuông DOC và tam giác vuông DOE có :
OD chung
OC = OE ( tam giác vuông AOC = tam giác vuông BOE )
\(\implies\) tam giác vuông DOC = tam giác vuông DOE ( 2 cạnh góc vuông )
\(\implies\) CD = ED ( 2 cạnh tương ứng )
Mà ED = EB + BD
\(\implies\) ED = AC + BD
\(\implies\) CD = AC + BD
b) Xét tam giác DOE vuông tại O có :
OE2 + OD2 = DE2 ( Theo định lý Py - ta - go )
Xét tam giác BOE vuông tại B có :
OB2 + BE2 = OE2 ( Theo định lý Py - ta - go ) ( * )
Xét tam giác BOD vuông tại B có :
OB2 + BD2 = OD2 ( Theo định lý Py - ta - go ) ( ** )
Cộng ( * ) với ( ** ) vế với vế ta được :
OE2 + OD2 = 2. OB2 + EB2 + DB2
Mà OE2 + OD2 = DE2 ( cmt )
\(\implies\) DE2 = 2. OB2 + EB2 + DB2
= 2. OB2 + EB . ( DE - BD ) + DB . ( DE - BE )
= 2. OB2 + EB . DE - EB . BD + DB . DE - DB . BE
= 2. OB2 + ( EB . DE + DB . DE ) - 2 . BD . BE
= 2. OB2 + DE . ( EB + DB ) - 2 . BD . BE
= 2. OB2 + DE2 - 2 . BD . BE
\(\implies\) 2. OB2 - 2 . BD . BE = 0
\(\implies\) 2. OB2 = 2 . BD . BE
\(\implies\) OB2 = BD . BE
Mà BE = AC ( cmt ) ; OB = AB / 2 ( gt )
\(\implies\) AC . BD = ( AB / 2 )2
\(\implies\) AC . BD = AB2 / 4
8 tháng 1 2022
a: Xét tứ giác ACBD có
AC//BD
AC=BD
Do đó: ACBD là hình bình hành
Suy ra: AD=BC
b: Ta có: ACBD là hình bình hành
nên AD//BC
c:
Ta có: CE+EB=CB
FD+AF=AD
mà CB=AD
và CE=FD
nên EB=AF
Xét tứ giác EBFA có
EB//AF
EB=AF
Do đó: EBFA là hình bình hành
Suy ra:EF và BA cắt nhau tại trung điểm của mỗi đường
mà O là trung điểm của AB
nên O là trung điểm của FE
13 tháng 6 2023
1: Xét tứ giác ACBD có
AC//BD
AC=BD
=>ACBD là hbh
=>O là trung điểm chung của AB và CD
2: Xét tứ giác AEBF có
AF//BE
AF=BE
=>AEBF là hbh
=>O là trung điểm của EF
14 tháng 4 2020
Mình cũng đang cần . Ai bt chỉ mình với , link cũng đc nhé. Thank you.
28 tháng 3 2023
1:Gọi giao của DO và CB là H
Xét ΔOAD vuông tại A và ΔOBH vuông tại B có
OA=OB
góc AOD=góc BOH
=>ΔOAD=ΔOBH
=>OD=OH
=>ΔCDH cân tại C
=>ΔAOD đồng dạng với ΔBOH
Xét ΔBOH vuông tại B và ΔOCH vuông tại O có
góc BHO chung
=>ΔBOH đồng dang với ΔOCH
=>ΔAOD đồng dạng với ΔOCH
2: ΔCHD cân tại C
=>góc CDH=góc CHD=góc ADH
=>DH là phân giác của góc ADC
