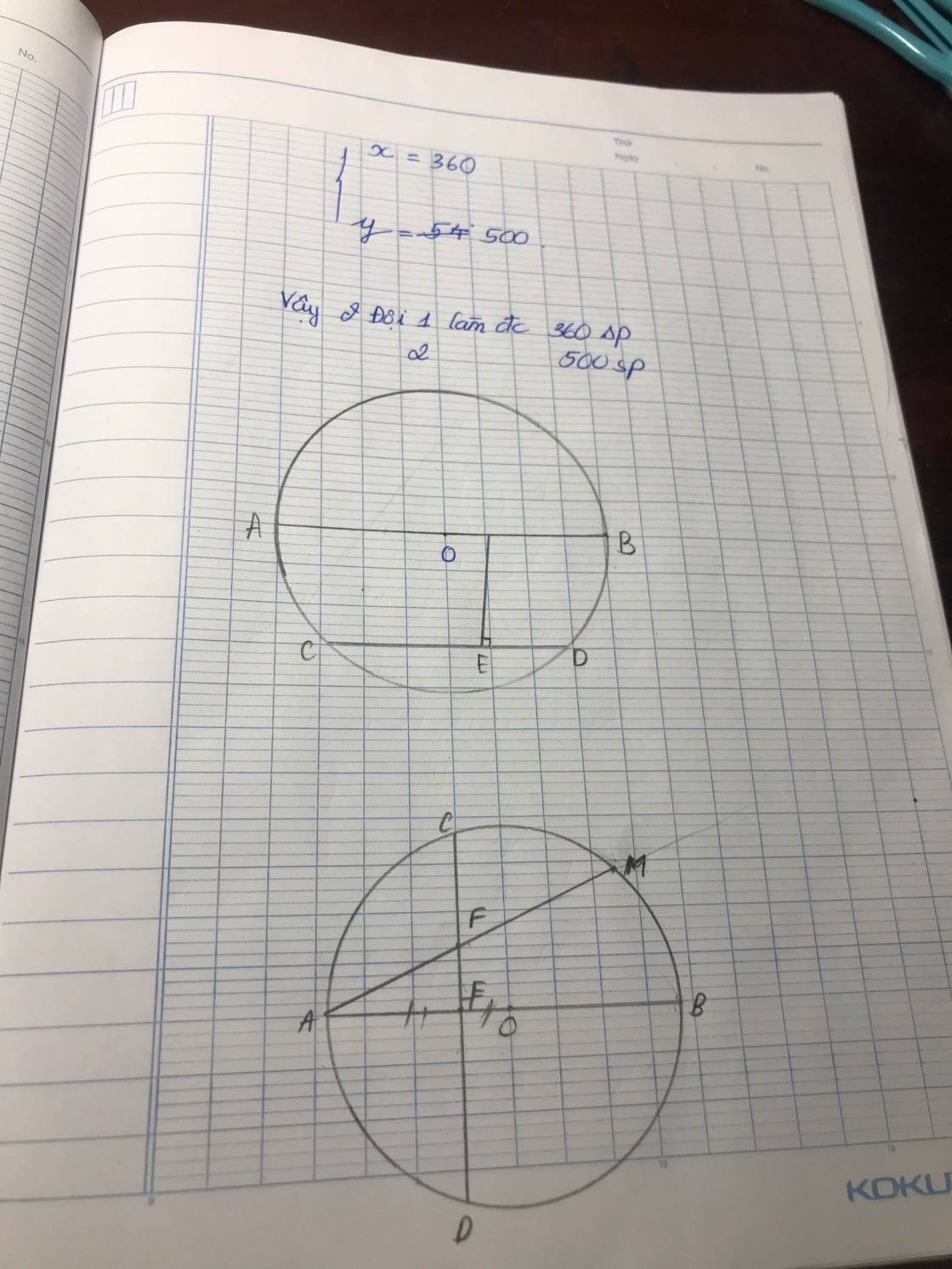
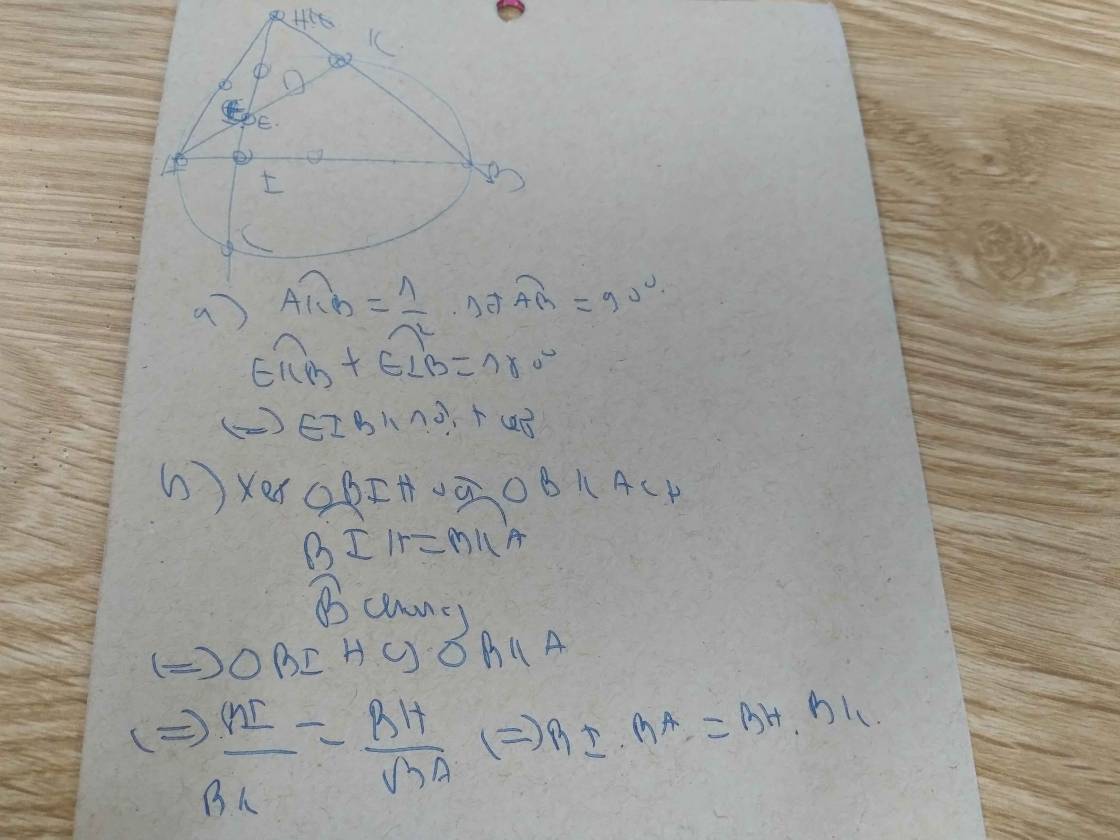(4,0 điểm) Cho đường tròn $(O)$ đường kính $AB$. Dây $CD$ vuông góc với $AB$ tại $E$ ($E$ nằm giữa $A$ và $O$; $E$ không trùng với $A$ và $O$). Lấy điểm $M$ thuộc cung nhỏ $BC$ sao cho cung $MB$ nhỏ hơn cung $MC$. Dây $AM$ cắt $CD$ tại $F$. Tia $BM$ cắt đường thẳng $CD$ tại $K$.
1. Chứng minh tứ giác $BMFE$ nội tiếp.
2. Chứng minh $BF$ vuông góc với $AK$ và $EK.EF=EA.EB$.
3. Tiếp tuyến của $(O)$ tại $M$ cắt tia $KD$ tại $I$. Chứng minh $IK=IF$.