Chứng minh:a2+5b2-(3a+b)\(\ge\)3ab-5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 3 2018
Links:
Chứng minh $a^2+5b^2-(3a+b)\geq 3ab-5$ - Bất đẳng thức và cực trị - Diễn đàn Toán học
Chứng minh a^2 + 5b^2 - (3a + b) ≥ 3ab - 5 - Toán học Lớp 8 - Bài tập Toán học Lớp 8 - Giải bài tập Toán học Lớp 8 | Lazi.vn - Cộng đồng Tri thức & Giáo dục
LA
14 tháng 12 2017
\(a^2+5b^2-\left(3a+b\right)\ge3ab-5\)
\(\Leftrightarrow2a^2+10b^2-2\left(3a+b\right)\ge6ab-10\)
\(\Leftrightarrow2a^2+10b^2-6a-2b-6ab+10\ge0\)
\(\Leftrightarrow\left(a^2-6a+9\right)+\left(b^2-2b+1\right)+\left(a^2-6ab+9b^2\right)\ge0\)
\(\Leftrightarrow\left(a-3\right)^2+\left(b-1\right)^2+\left(a-3b\right)^2\ge0\)
\(\Leftrightarrowđcpm\)
PT
0
22 tháng 3 2018
1a)\(\dfrac{a^2+b^2}{2}\ge\dfrac{\left(a+b\right)^2}{4}\)
\(\Leftrightarrow2\left(a^2+b^2\right)\ge\left(a+b\right)^2\)
\(\Leftrightarrow a^2-2ab+b^2\ge0\)
\(\Leftrightarrow\left(a-b\right)^2\ge0\)(luôn đúng)
b)\(\dfrac{a^2+b^2+c^2}{3}\ge\dfrac{\left(a+b+c\right)^2}{9}\)
\(\Leftrightarrow3\left(a^2+b^2+c^2\right)\ge\left(a+b+c\right)^2\)
\(\Leftrightarrow2a^2+2b^2+2c^2-2ab-2ac-2bc\ge0\)
\(\Leftrightarrow\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)+\left(c^2-2ca+a^2\right)\ge0\)
\(\Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\)(luôn đúng)
22 tháng 3 2018
2a)\(a^2+\dfrac{b^2}{4}\ge ab\)
\(\Leftrightarrow a^2-ab+\dfrac{b^2}{4}\ge0\)
\(\Leftrightarrow a^2-2\cdot\dfrac{1}{2}b\cdot a+\left(\dfrac{1}{2}b\right)^2\ge0\)
\(\Leftrightarrow\left(a-\dfrac{1}{2}b\right)^2\ge0\)(luôn đúng)
b)Đã cm
c)\(a^2+b^2+1\ge ab+a+b\)
\(\Leftrightarrow2a^2+2b^2+2\ge2ab+2a+2b\)
\(\Leftrightarrow\left(a^2-2ab+b^2\right)+\left(a^2-2a+1\right)+\left(b^2-2b+1\right)\ge0\)
\(\Leftrightarrow\left(a-b\right)^2+\left(a-1\right)^2+\left(b-1\right)^2\ge0\)(luôn đúng)
Dấu bằng xảy ra khi a=b=1
N
1
NN
22 tháng 4 2017
1. Ta có:
\(a^2+5b^2-\left(3a+b\right)\ge3ab-5\)
\(\Leftrightarrow2a^2+10b^2-6a-2b-6ab+10\ge0\)
\(\Leftrightarrow a^2-6ab+9b^2+a^2-6a+9+b^2-2b+1\ge0\)
\(\Leftrightarrow\left(a-3b\right)^2+\left(a-3\right)^2+\left(b-1\right)^2\ge0\)
Dấu "=" xảy ra khi \(\hept{\begin{cases}a=3\\b=1\end{cases}}\)
2. Giải:
Ta có: \(2x^2+3y^2+4x=19\)
\(\Leftrightarrow2x^2+4x+2=21-3y^2\)
\(\Leftrightarrow2\left(x+1\right)^2=3\left(7-y^2\right)\left(1\right)\)
Xét thấy \(VT⋮2\Leftrightarrow3\left(7-y^2\right)⋮2\Leftrightarrow y\) lẻ (2)
Mặt khác \(VT\ge0\Leftrightarrow3\left(7-y^2\right)\ge0\Leftrightarrow y^2\le7\) (3)
Kết hợp (2) và (3) suy ra:
\(y^2=1\) Thay vào \(\left(1\right)\) ta có:
\(2\left(x+1\right)^2=18\). Vậy ta tính được các nghiệm:
\(\left(x,y\right)=\left(2;1\right);\left(2;-1\right);\left(-4;-1\right);\left(-4;1\right)\)
HF
24 tháng 10 2019
\(\sqrt{a^2+3a+5}\ge\frac{5a+13}{6}\Leftrightarrow a^2+3a+5\ge\frac{25a^2+130a+169}{36}\)
\(\Leftrightarrow36a^2+108a+180\ge25a^2+130a+169\Leftrightarrow11a^2-22a+11\ge0\)
\(\Leftrightarrow11\left(a-1\right)^2\ge0\forall a\inℝ\)
Dấu = xảy ra khi a=1
24 tháng 10 2019
Ta có:
\(\sqrt{a^2+3ab+5b^2}=\sqrt{\left(\frac{25a^2}{36}+\frac{130ab}{36}+\frac{169}{36}\right)+\frac{11}{36}\left(a^2-2ab+b^2\right)}\)
\(=\sqrt{\left(\frac{5a}{6}+\frac{13b}{6}\right)^2+\frac{11}{36}\left(a-b\right)^2}\ge\frac{5a+13b}{6}\)
Tương tự:\(\sqrt{b^2+3bc+5c^2}\ge\frac{5b+13c}{6};\sqrt{c^2+3ca+5a^2}\ge\frac{5c+13a}{6}\)
Khi đó:\(P=\sqrt{a^2+3ab+5b^2}+\sqrt{b^2+3bc+5c^2}+\sqrt{c^2+3ac+5a^2}\)
\(\ge\frac{5a+13b+5b+13c+5c+13a}{6}=\frac{18\left(a+b+c\right)}{6}=3\left(a+b+c\right)=9\)
Dấu "=" xảy ra tại \(a=b=c=1\)
10 tháng 9 2018
\(a^2+b^2+3ab⋮5\)
\(\Leftrightarrow6a^2+12ab+6b^2⋮5\)
\(\Leftrightarrow\left(2a+3b\right)\left(3a+2b\right)⋮5\)
Giả sử \(2a+3b⋮5\) (1)
Mà \(9\left(2a+3b\right)-\left(3a+2b\right)=15a+25b⋮5\)
\(\Rightarrow3a+2b⋮5\) (2)
Mặt khác 5 là số nguyên tố (3)
Từ (1)(2)(3) \(\Rightarrow\left(2a+3b\right)\left(3a+2b\right)⋮25\)
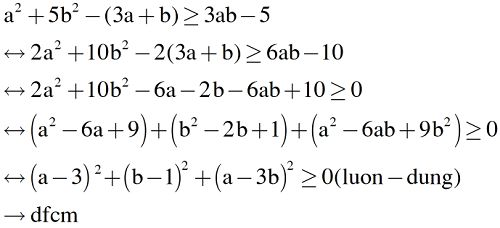
\(a^2+5b-\left(3a+b\right)\ge3ab-5\)
\(\Leftrightarrow2a^2+10b^2-6a-2b-6ab+10\ge0\)
\(\Leftrightarrow\left(a^2-6ab+9b^2\right)+\left(a^2-6a+9\right)+\left(b^2-2b+1\right)\ge0\)
\(\Leftrightarrow\left(a-3b\right)^2+\left(a-3\right)^2+\left(b-1\right)^2\ge0\)
Đẳng thức xảy ra khi \(\hept{\begin{cases}a-3b=0\\a-3=0\\b-1=0\end{cases}}\)\(\Rightarrow\hept{\begin{cases}a=3\\b=1\end{cases}}\)
Dễ thế này cũng hỏi nổi, LẠY @@