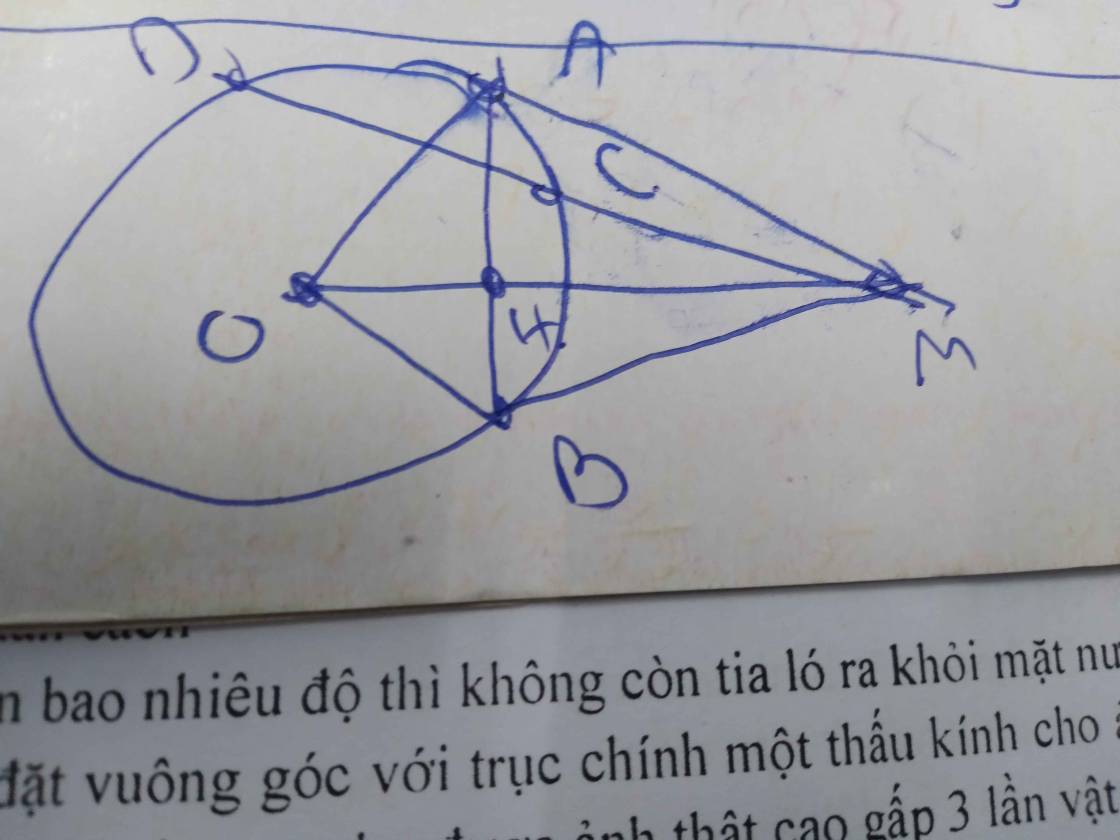
Cho đường tròn tâm O và điểm M nằm ngoài đường tròn , vẽ các tiếp tuyến MA,MB với đường tròn (O) ,(AB là các tiếp điểm ) và cát tuyến MCD không đi qua tâm O(MC,<MD, A và O nằm khác phía có bờ la CD ),gọi I là trung điểm của CD
a. Chứng minh 5 điểm M,A,I,O,B cùng thuộc một đường tròn
b. Chứng minh MA2= MC.MD


a: ΔOCD can tại O
mà OI là trung tuyến
nên OI vuông góc CD
Xét tứ giác OAMB có
góc OAM+góc OBM=180 độ
=>OAMB là tứ giác nội tiếp
=>O,A,M,B cùng thuộc 1 đường tròn đường kính OM(1)
Vì ΔOIM vuông tại I
nên I nằm trên đường tròn đường kính OM(2)
Từ (1), (2) suy ra ĐPCM
b: Xét ΔMAC và ΔMDA có
góc MAC=góc MDA
góc AMC chung
=>ΔMAC đồng dạng vơi ΔMDA
=>MA/MD=MC/MA
=>MA^2=MD*MC