Không cần tính tổng phân số chứng tỏ A<2, biết A= 11/29+9/17+10/19
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
DT
0

VN
11


29 tháng 2 2016
Ta có:\(\frac{11}{29}\)<1
\(\frac{9}{17}\)<1 và\(\frac{10}{19}\)<1
=>A=\(\frac{11}{29}+\frac{9}{17}+\frac{10}{19}\)<1
=>A<2

AH
Akai Haruma
Giáo viên
29 tháng 1 2022
Bài 4:
$A+2=1+2+2^2+2^3+...+2^{11}$
$=(1+2)+(2^2+2^3)+....+(2^{10}+2^{11})$
$=(1+2)+2^2(1+2)+....+2^{10}(1+2)$
$=(1+2)(1+2^2+....+2^{10})$
$=3(1+2^2+...+2^{10})\vdots 3$
Vậy $A+2\vdots 3$ nên $A$ không chia hết cho $3$
AH
Akai Haruma
Giáo viên
29 tháng 1 2022
Bài 5:
$n^2+n+1=n(n+1)+1$
Vì $n,n+1$ là hai số tự nhiên liên tiếp nên sẽ tồn tại một số chẵn và 1 số lẻ
$\Rightarrow n(n+1)$ chẵn
$\Rightarrow n^2+n+1=n(n+1)+1$ lẻ (điều phải chứng minh)
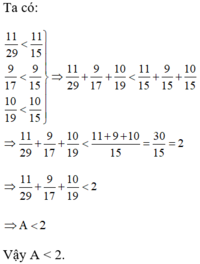
vì các tử trên đều nhỏ hơn mẫu
mà các tử bé hơn mẫu thì đều bé hơn 1 nên A sẽ bé hơn 2