Chứng minh rằng trong một tam giác hai đường phân giác 2 góc ngoài của tam giác và đường phân giác trong của đỉnh còn lại đồng quy.
(vẽ hình và ghi lời giải đầy đủ, ban nào làm xong sớm và đúng mình sẽ tick)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
13 tháng 4 2017
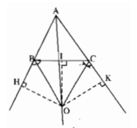
Giả sử hai tia phân giác của các góc ngoài tại đỉnh B và C của tam giác ABC cắt nhau tại O. Ta sẽ chứng minh AO là tia phân giác của góc A.
Kẻ các đường vuông góc OH, OI, OK từ O lần lượt đến các đường thẳng AB, BC, AC.
Vì BO là tia phân giác của góc HBC nên OH = OI (1)
Vì CO là tia phân giác của góc KCB nên OI = OK (2)
Từ (1) và (2) suy ra OI = OH = OK
(3)
Suy ra: O thuộc đường phân giác của góc BAC.
Suy ra AO là tia phân giác của góc BAC và ta có điều phải chứng minh.
LV
8 tháng 8 2021
Gọi I là giao của ∠ABC và ∠ACB, gọi D, F, E lần lượt là hình chiếu của I trên
AC, AB, BC
Xét ∆FBI và ∆EBI:
∠FBI=∠IBE(gt)
BI chung
∠BFI=∠IEB=900(gt) =>∆FBI = ∆EBI(g-c-g)
Do đó IF=IE(cạnh tương ứng)
Xét ∆FAI và ∆DAI:
∠FAI=∠IAD(gt)
AI chung
∠AFI=∠IDA=900(gt) =>∆FAI = ∆DAI(g-c-g)
Do đó IF=ID(cạnh tương ứng)
IF=ID;IF=IE =>ID=IE
Xét ∆ECI và ∆DCI:
∠IEC=∠IDC=900(gt)
ID=IE(CMT)
CI chung => ∆ECI = ∆DCI (cạnh huyền -cạnh góc vuông)
Do đó : ∠ECI=∠ICD
=>IC là phân giác góc BCA
Vậy ba đường phân giác trong CI, AI, BI đồng quy tại một diểm
ED
4 tháng 3 2016
ai kết bạn với mik nha
fan MTP
ai chơi truy kích kết ban lun nha
H
21 tháng 4 2022
Tham khảo
Gọi E, F, P lần lượt là hình chiếu của I trên các đường thẳng AB, BC, CA.
Theo Định lí thuận ta có IE = IF và IF = IP => IE = IP .
Vậy I cách đều hai cạnh AB, AC.
25 tháng 3 2023
BM,BN là phân giác của hai góc kề bù
=>góc MBN=90 độ
CM,CN là phân giác của haigóc kề bù
=>góc MCN=90 độ
Vì góc MBN+góc MCN=180 độ
nên MBNC nội tiếp
LV
8 tháng 8 2021
Gọi I là giao của ∠ABC và ∠ACB, gọi D, F, E lần lượt là hình chiếu của I trên
AC, AB, BC
Xét ∆FBI và ∆EBI:
∠FBI=∠IBE(gt)
BI chung
∠BFI=∠IEB=900(gt) =>∆FBI = ∆EBI(g-c-g)
Do đó IF=IE(cạnh tương ứng)
Xét ∆FAI và ∆DAI:
∠FAI=∠IAD(gt)
AI chung
∠AFI=∠IDA=900(gt) =>∆FAI = ∆DAI(g-c-g)
Do đó IF=ID(cạnh tương ứng)
IF=ID;IF=IE =>ID=IE
Xét ∆ECI và ∆DCI:
∠IEC=∠IDC=900(gt)
ID=IE(CMT)
CI chung => ∆ECI = ∆DCI (cạnh huyền -cạnh góc vuông)
Do đó : ∠ECI=∠ICD
=>IC là phân giác góc BCA
Vậy ba đường phân giác trong CI, AI, BI đồng quy tại một diểm
