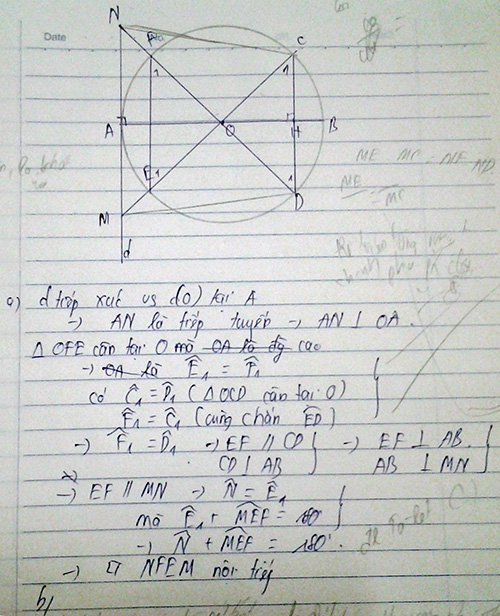Cho (O:R) đường kính AB. Điểm H thuộc OB ( H không trùng O và B). Dây CD vuông góc với AB tại H, đường thẳng d tiếp xúc với đường tròn tại A. CO,DO cắt đường thằng d lần lượt tại M,N. CM và DN cắt đường tròn (O) lần lượt tại E,F.
a) Chứng minh tứ giác MNEF nội tiếp
b) chứng minh ME.MC=NF.ND
c)Tìm bị trí của H để tứ giác AEOF là hình thoi
d) Lấy K đối xứng cới C qua A. Gọi G là trọng tâm của tam giác KAB. Chứng minh rằng khi H chuyển động trên OB thì G thuộc 1 đường tròn cố định.