Cho tứ giác lồi ABCD về phía trong tứ giác ta dựng các nửa đường tròn đường kính là các cạnh của tứ giác . Chứng minh rằng tứ giác ABCD hoàn toàn bị phủ kín bởi 4 nửa đường tròn trên.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
3 tháng 1 2017
Đặt AB = a; BC = b; CD = c; AD = d
C A B 2 = 2 π . a 2 2 = π . a 2 . Tương tự C C D 2 = π . c 2
Vậy C A B 2 + C C D 2 = π 2 a + c
Có C B C 2 + C C D 2 = π 2 b + d
Tứ giác ABCD ngoại tiếp, kết hợp tính chất tiếp => a + c = b + d => ĐPCM
TA
22 tháng 3 2016
Giả sử tứ giác ABCD định hướng âm. Gọi \(f\) là phép quay vec tơ theo góc \(\frac{\pi}{3}\) ta có
\(\overrightarrow{EG}=\overrightarrow{AG}-\overrightarrow{AE}=\overrightarrow{AB}+\overrightarrow{BG}-\overrightarrow{AE}\)
suy ra \(f\left(\overrightarrow{EG}\right)=f\left(\overrightarrow{AB}\right)+f\left(\overrightarrow{BG}\right)-f\left(\overrightarrow{AE}\right)\)
\(=\overrightarrow{AE}+\overrightarrow{BC}-\overrightarrow{BE}\)
\(=\overrightarrow{AC}\)
Tương tự ta cũng chứng minh được \(f\left(\overrightarrow{HF}\right)=\overrightarrow{AC}\)
Từ đó suy ra \(\overrightarrow{EG}=\overrightarrow{HF}\)
Do đó tứ giác EGFH là hình bình hành
11 tháng 4 2023
Ta có : A là giao điểm của 2 đường tiếp tuyến tại E và G của O =>AG=AE
Chứng minh tương tự,ta được BE=BH
=>AG+BH=AB
Tương tự,ta có DG+HC=CD
=>AB+CD=AD+BC=10cm
nửa đường tròn tâm G: 2AG.π/2=AG.π=1/2.AD.π
nửa đường tròn tâm H:1/2.BC.π
=> S=1/2(AD+BC)π=5π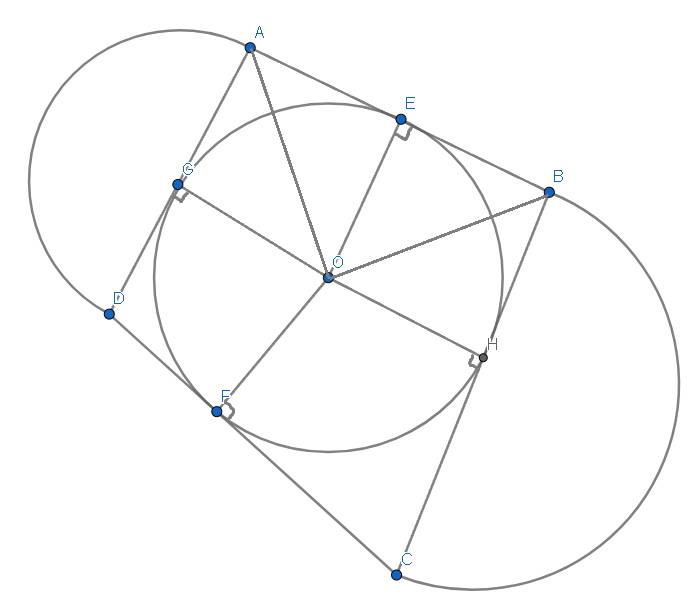
AH
Akai Haruma
Giáo viên
12 tháng 7 2021
Lời giải:
1.
$\widehat{MDC}=90^0$ (góc nt chắn nửa đường tròn)
$\Leftrightarrow \widehat{BDC}=90^0$
Tứ giác $ABCD$ có $\widehat{BAC}=\widehat{BDC}=90^0$ và cùng nhìn cạnh $BC$ nên là tgnt.
Do $ABCD$ nội tiếp nên $\widehat{BCA}=\widehat{BDA}$
Mà $\widehat{BDA}=\widehat{MCS}$ (do $MDSC$ nội tiếp)
$\Rightarrow \widehat{BCA}=\widehat{MCS}$
$\Rightarrow CA$ là phân giác $\widehat{BCS}$
2.
Gọi $T$ là giao điểm của $BA$ và $EM$
Xét tam giác $BTC$ có $TE\perp BC$ (do $\widehat{MEC}=90^0$) và $CA\perp BT$ và $TE, CA$ giao nhau tại $M$ nên $M$ là trực tâm tam giác $BTC$
$\Rightarrow BM\perp TC$.
Mà $BM\perp DC$ nên $TC\parallel DC$ hay $T,D,C$ thẳng hàng
Do đó $BA, EM, DC$ đồng quy tại $T$
3.
Vì $ABCD$ nt nên $\widehat{MAD}=\widehat{CAD}=\widehat{DBC}=\widehat{MBE}$
Dễ cm $BAME$ nội tiếp cho $\widehat{A}+\widehat{E}=90^0+90^0=180^0$ nên $\widehat{MBE}=\widehat{EAM}$
Do đó: $\widehat{MAD}=\widehat{EAM}$ nên $AM$ là tia phân giác $\widehat{EAM}(*)$
Mặt khác:
Cũng do $MECD,ABCD$ nội tiếp nên:
$\widehat{ADM}=\widehat{ADB}=\widehat{ACB}=\widehat{MCE}=\widehat{MDE}$
$\Rightarrow DM$ là tia phân giác $\widehat{ADE}(**)$
Từ $(*); (**)\Rightarrow M$ là tâm đường tròn nội tiếp $ADE$.
CM
19 tháng 6 2019
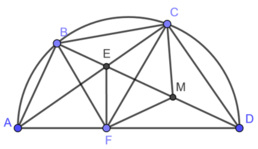
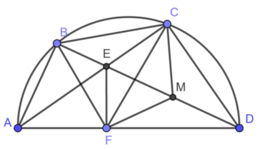
Xét tam giác vuông EFD có:
FM là đường trung tuyến ứng với cạnh huyền CD
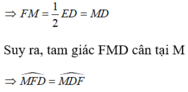
Ta có:
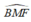là góc ngoài tại đỉnh M của tam giác FMD nên:
Xét tứ giác BCMF có:
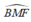và 
và cùng nhìn cạnh BF dưới một góc bằng nhau
Suy ra, tứ giác BCMF nội tiếp được.
