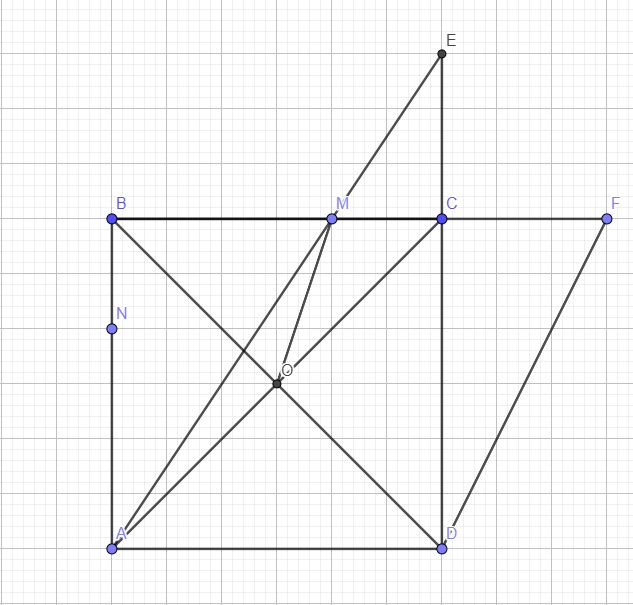
Cho hình vuông ABCD. Trên cạnh AB lấy điểm M, trên tia đối của CB lấy điểm N sao cho AM =CN . Gọi Ilà giao điểm của MN và CD.
GọI E là trung điểm của MN, tia DE cắt BC tại F. Qua M vẽ đường thẳng song song với AD cắt DF tại H.
Chứng minh rằng : Tứ giác MFNH là hình thoi.
Chứng minh : Chu vi tam giác BMF không đổi khi m di động trên cạnh AB.