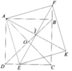
Cho hình vuông ABCD. Trên cạnh BC lấy điểm E, trên tia đối của DC, lấy điểm F sao cho FAD = EABa) Chứng minh: ΔAFD = ΔAEBb) Gọi I là trung điểm của EF, M là giao điểm của AI và CD. Qua E kẻ đường thẳ...

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

H

Hikari

18 tháng 1 2023

Cho hình vuông ABCD. Trên cạnh BC lấy điểm E, trên tia đối của DC, lấy điểm F sao cho FAD = EABa) Chứng minh: ΔAFD = ΔAEBb) Gọi I là trung điểm của EF, M là giao điểm của AI và CD. Qua E kẻ đường thẳng song song với CD và cắt AI tại N. Chứng minh: AI vuông góc EF và tứ giác MENF là hình thoic) Chứng minh: S(AME) = S(ADM) +...

1

NL

Nguyễn Lê Phước Thịnh

18 tháng 1 2023

a: Xét ΔAFD vuông tại D và ΔAEB vuông tại B có

AD=AB

góc FAD=góc EAB

Do đó: ΔAFD=ΔAEB

b: ΔAFD=ΔAEB

=>AF=AE

=>ΔAFE cân tại A

mà AI là trung tuyến

nên AI vuông góc với EF

Xét ΔINE vuông tại I và ΔIMF vuông tại I có

IE=IF
góc IEN=góc IFM

Do đó: ΔINE=ΔIMF

=>IN=IM

Xét tứ giác MFNE có

I là trung điểm chung của MN và FE

MN vuông góc với FE

Do đó: MFNE là hình thoi

Những câu hỏi liên quan

CT

Cam Tu

13 tháng 10 2021

Cho tam giác ABC vuông cân tại A. Trên tia đối của tia CA lấy điểm F; trên tia đối của tia AB lấy điểm E sao cho BE = CF. Vẽ hình bình hành BEFD. a) Chứng minh DC ⊥ BC. b) Gọi I là giao EF và BC. Chứng minh AI = 1 2 DB. c) Qua I kẻ đường thẳng vuông góc với AF cắt BD tại M. Chứng minh MICF là hình thang cân. d) Tìm vị trí của E trên AB để A, I, D thẳng...

0

PT

Pham Trong Bach

9 tháng 3 2018

Cho hình vuông ABCD. E là điểm trên cạnh DC, F là điểm trên tia đối của tia BC sao cho BF = DE.

a) Chứng minh tam giác AEF vuông cân.

b) Gọi I là trung điểm của EF. Chứng minh I thuộc BD.

c) Lấy điểm K đối xứng với A qua I. Chứng minh tứ giác AEKF là hình vuông

1

CM

Cao Minh Tâm

9 tháng 3 2018

a) DDAE = DBAF (c.g.c)

⇒ D A E ^ = B A F ^ và AE = AF

Mà E A D ^ + E A B ^ = 90 0 = > E A B ^ + B A F ^ = 90 0

Þ DAEF vuông cân tại A.

b) DEAF vuông cân nên IA = IE = FI (1); DCFE vuông có IC là đường trung tuyến Þ IE = IC = IF (2);

Từ (1) và (2) suy ra Þ IA = IC nên I thuộc trung trực của AC hay I thuộc BD.

c) Do K đối xứng với A qua I nên I là trung điểm của AK.

Mà I là trung điểm của EF(gt) nên AFKE là hình bình hành, DAEF vuông cân tại A nên AI ^ EF.

Vậy AFKE là hình vuông.

DT

Đặng Thụy Thiên

26 tháng 12 2021

Cho hình vuông ABCD, E là điểm trên cạnh DC, F là điểm trên tia đối của tia BC sao cho BF = DE.

a) Chứng minh tam giác AEF vuông cân.

b) Gọi I là trung điểm của EF .Chứng minh I thuộc BD.

c) Lấy điểm K đối xứng với A qua I.Chứng minh tứ giác AEKF là hình vuông.

1

UT

Uyên Thy

26 tháng 12 2021

a, Xét 2 tam giác vuông ΔADE và ΔABF có:

AD = AB (ABCD là hình vuông); DE = BF (gt)

⇒ ΔADE = ΔABF (2 cạnh góc vuông)

⇒ AE = AF (1) và $\hat{D A E}$ = $\hat{B A F}$

mà $\hat{D A E}$ + $\hat{B A E}$ = $90^{o}$

⇒ $\hat{B A F}$ + $\hat{B A E}$ = $90^{o}$

⇒ $\hat{E A F}$ = $90^{o}$ (2)

Từ (1) và (2) suy ra ΔEAF vuông cân (đpcm)

b, ABCD là hình vuông ⇒ BA = BC và DA = DC

⇒ BD là đường trung trực của AC (3)

ΔEAF vuông cân tại A có AI là trung tuyến ứng với cạnh huyền

⇒ AI = $\frac{1}{2}$ EF

ΔCEF vuông tại C có CI là trung tuyến ứng với cạnh huyền

⇒ CI = $\frac{1}{2}$ EF

⇒ CI = AI ⇒ I thuộc đường trung trực của AC (4)

Từ (3) và (4) suy ra: I thuộc BD (đpcm)

d, Tứ giác AEKF có 2 đường chéo AK, EF cắt nhau tại I là trung điểm mỗi đường

⇒ AEKF là hình bình hành

mà AE = AF và $\hat{E A F}$ = $90^{o}$

⇒ AEKF là hình vuông (đpcm)

NV

Ngân Vũ

2 tháng 5 2016 - olm

Cho hình vuông ABCD trên cạnh BC lấy điểm E. Từ A kẻ đường thẳng vuông góc vơi AE cắt đường thẳng CD tại F. Gọi I là trung điểm của EF. AI cắt CD tại M. Qua E dựng đường thẳng song song với CD cắt AI tại N.a) Chứng minh tứ giác MENF là hình thoi.b) Chứng minh chi vi tam giác CME không đổi khi E chuyển động trên BCCho hình vuông ABCD trên cạnh BC lấy điểm E. Từ A kẻ đường thẳng vuông góc vơi AE...

0

2D

2K9-(✎﹏ ΔΠGΣLS ΩҒ DΣΔTH )

19 tháng 1 2023 - olm

Cho hình vuông ABCD. Trên cạnh AB lấy điểm M, trên tia đối của CB lấy điểm N sao cho AM =CN . Gọi Ilà giao điểm của MN và CD. GọI E là trung điểm của MN, tia DE cắt BC tại F. Qua M vẽ đường thẳng song song với AD cắt DF tại H. Chứng minh rằng : Tứ giác MFNH là hình thoi. Chứng minh : Chu vi tam giác BMF không đổi khi m di động trên cạnh...

0

B

Blal

26 tháng 12 2020

Cho hình vuông ABCD cạnh AB =a.Trên cạnh DC lấy điểm M và trên tia đối của tia BC lấy điểm N sao cho DM=BN. a)Chứng minh AM=AN b)Gọi O là trung điểm của MN,K là điểm đối xứng với A qua O.Chứng minh tứ giác AMKN là hình vuông. c)Gọi E là giao điểm của AK và BC.Tính chu vi tam giác CME theo a? Giúp mình với

0