Cho nửa đường tròn (o), đường kính AB. Hai tiếp tuyến Ax, By trên cùng 1 mặt phẳng bờ AB chứa nửa đường tròn (o). Tiếp tuyến tại điẻm M của nửa đường tròncắt Ax tại C và By tại D
a) COD là tam giác gì?
b) C/m: CD=AB+BD
c) AM và BM cắt OC và OD lần lượt tại E và F. Tứ giác OEMF là hình gì?
d) Gọi I là giao điểm 2 đường chéo OM và EF của tứ giác OEMF. Khi M thay đổi trên nửa đường tròn (o) thì điểm I chuyển động trên đường nào? Vì sao?
e) Xác định vị trí của M để tứ giác OEMF là hình vuông? Tính diện tích của hình vuông này. Cho biết AB=6cm

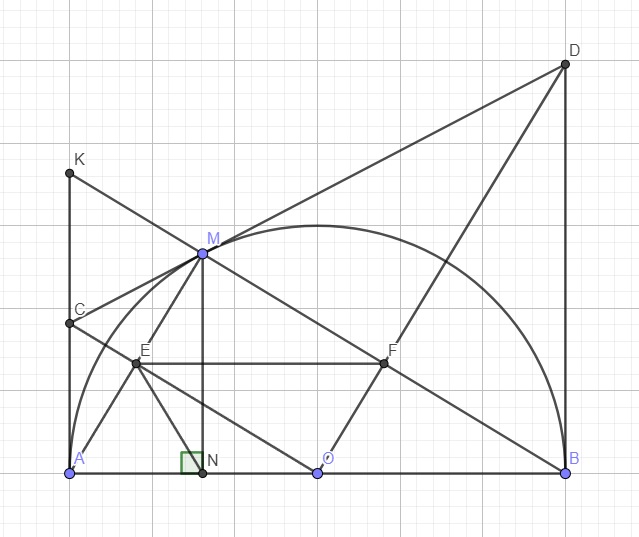
a: Xét (O) có
CM,CA là tiếp tuyến
nen CM=CA và OC là phân giác của góc MOA(1)
mà OM=OA
nên OC là trung trực của AM
Xét (O) có
DM,DB là tiếp tuyến
nên DM=DB và OD là phân giác của góc MOB(2)
mà OM=OB
nên OD là trung trực của MB
Từ (1), (2) suy ra góc COD=1/2*180=90 độ
b: CD=CM+MD
=>CD=AC+BD
c: Xét tứ giác OEMF có
góc OEM=góc OFM=góc EOF=90 độ
nên OEMF là hình chữ nhật