tìm a, b, c, d biết :
x4 + ax3 + bx2 -8x + 4= ( x2 + cx + d)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
N
20 tháng 11 2021
Đặt \(g\left(x\right)=f\left(x\right)-10\) (bậc 4)
\(\Leftrightarrow\left\{{}\begin{matrix}g\left(1\right)=0\\g\left(2\right)=0\\g\left(3\right)=0\end{matrix}\right.\Leftrightarrow g\left(x\right)=\left(x-1\right)\left(x-2\right)\left(x-3\right)\left(x-m\right)\) (m là hằng số)
\(\Leftrightarrow f\left(x\right)=\left(x-1\right)\left(x-2\right)\left(x-3\right)\left(x-m\right)-10\\ \Leftrightarrow f\left(9\right)=8\cdot7\cdot6\left(9-m\right)-10=336\left(9-m\right)-10\\ f\left(-5\right)=\left(-6\right)\left(-7\right)\left(-8\right)\left(-5-m\right)-10=336\left(m+5\right)-10\)
Vậy \(A=336\left(9-m\right)+336\left(m+5\right)-20=4684\)
Chúc bạn hok tốt <3
CM
24 tháng 9 2018
Ta có f ( 0 ) = 0 f ( 1 ) = 0 f ' ( 0 ) = 0 f ' ( 1 ) = 0
↔ a = 2 b = - 3 c = 0 d = 1
, suy ra hàm số đã cho là : y= 2x3-3x2+ 1.
Ta thấy: f(x) = 0 ↔ x = 0 hoặc x = -1/2
Bảng biến thiên của hàm số y = |f(x)| như sau:
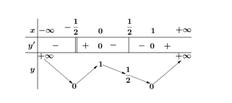
Dựa vào bảng biến thiên suy ra phương trình |f(x)| = m có bốn nghiệm phân biệt x1< x2< x3< ½< x4 khi và chỉ khi ½< m< 1.
Chọn A.
\
.
.
.
.
CM
12 tháng 3 2018
Đáp án B
Ta có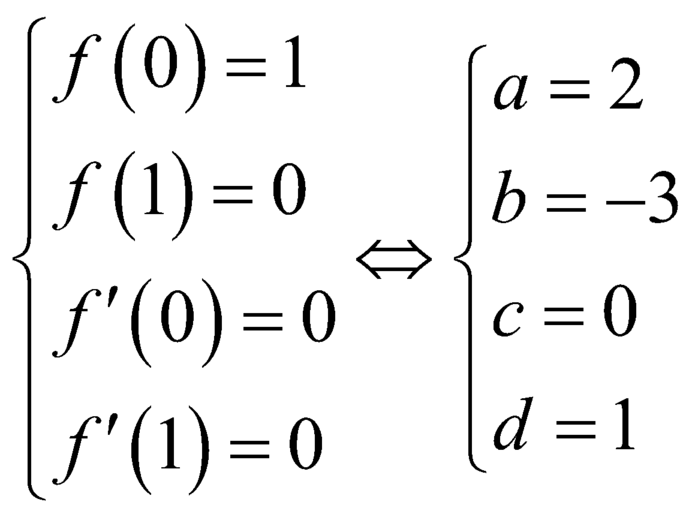 
suy ra 
.
Ta có: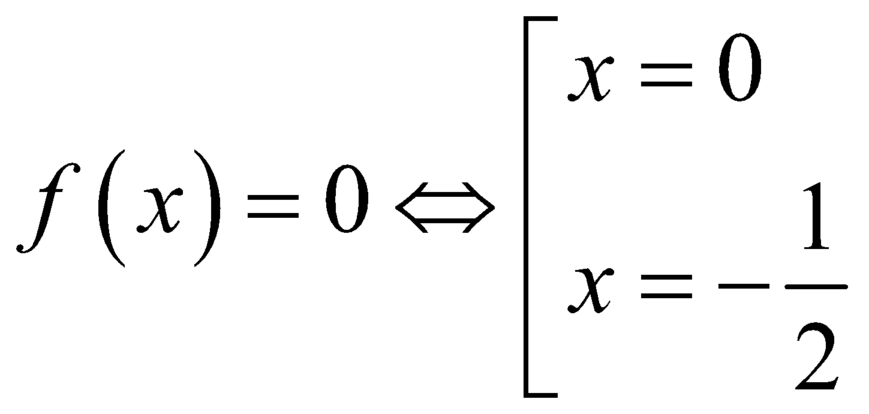 
.
Bảng biến thiên của hàm số 
như sau:
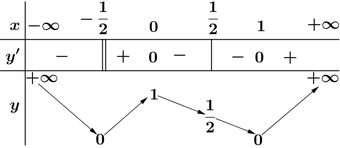
Dựa vào bảng biến thiên suy ra phương trình 
có bốn nghiệm phân biệt 
khi và chỉ khi 
.
AH
Akai Haruma
Giáo viên
30 tháng 4 2022
Bài 1:
1.
$6x^3-2x^2=0$
$2x^2(3x-1)=0$
$\Rightarrow 2x^2=0$ hoặc $3x-1=0$
$\Rightarrow x=0$ hoặc $x=\frac{1}{3}$
Đây chính là 2 nghiệm của đa thức
2.
$|3x+7|\geq 0$
$|2x^2-2|\geq 0$
Để tổng 2 số bằng $0$ thì: $|3x+7|=|2x^2-2|=0$
$\Rightarrow x=\frac{-7}{3}$ và $x=\pm 1$ (vô lý)
Vậy đa thức vô nghiệm.
AH
Akai Haruma
Giáo viên
30 tháng 4 2022
Bài 2:
1. $x^2+2x+4=(x^2+2x+1)+3=(x+1)^2+3$
Do $(x+1)^2\geq 0$ với mọi $x$ nên $x^2+2x+4=(x+1)^2+3\geq 3>0$ với mọi $x$
$\Rightarrow x^2+2x+4\neq 0$ với mọi $x$
Do đó đa thức vô nghiệm
2.
$3x^2-x+5=2x^2+(x^2-x+\frac{1}{4})+\frac{19}{4}$
$=2x^2+(x-\frac{1}{2})^2+\frac{19}{4}\geq 0+0+\frac{19}{4}>0$ với mọi $x$
Vậy đa thức khác 0 với mọi $x$
Do đó đa thức không có nghiệm.
BS
0
CM
13 tháng 3 2017
Đáp án C
Phương trình có ba nghiệm phân biệt nếu y c t < m < y c d ⇔ - 2 < m < 2
Hệ số của \(x^2+cx+d^2\) là \(d^2\)
\(\Rightarrow d^2=4\Rightarrow d=\pm2\)
Thay \(d=2\) vào biểu thức :
\(x^4+ax^3+bx^2-8x+4=x^2+cd+2\)
\(VP=x^2+cx+2=x^4+c^2x^2+4+2cx^3+4cx+4x^2=x^4+2cx^3++x^2+c^2+4++4cx+4\)
Ta có : \(x^4+2cx^3+x^2+c^2+4+4cx+4=x^4+ax^3+bx^2-8x+4\)
\(\left\{{}\begin{matrix}2c=a\\c^2+4=b\\4c=-8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}c=-2\\a=-4\\b=8\end{matrix}\right.\)
Tiếp tục thay \(d=-2\) tương tự \(d=2\)