Cho hình chóp tứ giác đều S.ABCD có đáy bằng a, và cạnh bên bằng a√2.
a) Tính thể tích của hình chóp đã cho.
b) Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD.
c) Gọi A’ và C' lần lượt là trung điểm của hai cạnh SA và SC. Chứng minh rằng hình chóp A’.ABCD và C’.CBAD bằng nhau.

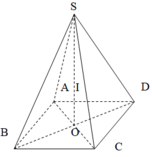
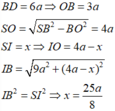
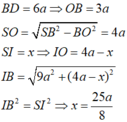
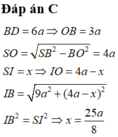
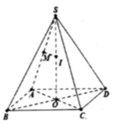
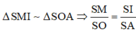
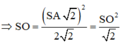
a) \(O\) là giao điểm của hai đường chéo của hình vuông \(ABCD\).
\(OC=\dfrac{1}{2}AC=\dfrac{1}{2}\sqrt{2}AB=\dfrac{a\sqrt{2}}{2}\)
\(SO=\sqrt{SC^2-OC^2}=\sqrt{\left(a\sqrt{2}\right)^2-\left(\dfrac{a\sqrt{2}}{2}\right)^2}=\dfrac{a\sqrt{6}}{2}\).
\(V_{S.ABCD}=\dfrac{1}{3}.SO.S_{ABCD}=\dfrac{1}{3}.\dfrac{a\sqrt{6}}{2}.a^2=\dfrac{a^3\sqrt{6}}{6}\)
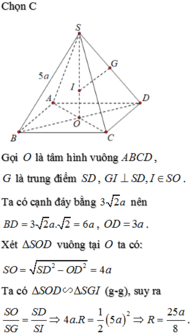
b) Gọi \(I\) là tâm mặt cầu ngoại tiếp hình chóp \(S.ABCD\).
Khi đó \(IA=IS\)
\(\Leftrightarrow\sqrt{OA^2+OI^2}=SO-OI\)
\(\Leftrightarrow\sqrt{\dfrac{a^2}{2}+OI^2}=\dfrac{a\sqrt{6}}{2}-OI\)
\(\Leftrightarrow\dfrac{a^2}{2}+OI^2=\left(\dfrac{a\sqrt{6}}{2}-OI\right)^2\)
\(\Leftrightarrow OI=\dfrac{a\sqrt{6}}{6}\).
Suy ra bán kính mặt cầu ngoại tiếp hình chóp \(S.ABCD\) là
\(SI=SO-OI=\dfrac{a\sqrt{6}}{2}-\dfrac{a\sqrt{6}}{6}=\dfrac{a\sqrt{6}}{3}\).
c) \(A'C'//AC\) suy ra \(A'C'\) vuông góc với mặt phẳng \(\left(SBD\right)\).
Mà \(A'C'\) cắt \(\left(SBD\right)\) tại trung điểm của nó nên \(C'\) đối xứng với \(A'\) qua mặt phẳng \(\left(SBD\right)\).
Tương tự \(A\) đối xứng với \(C\) qua mặt phẳng \(\left(SBD\right)\).
Suy ra phép đối xứng qua mặt phẳng \(\left(SBD\right)\) biến hình chóp \(A'.ABCD\) thành hình chóp \(C'.CBAD\) do đó hai hình chóp đó bằng nhau.