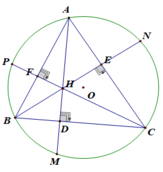
Cho tam giác ABC nhọn nội tiếp đường tròn (O). Các đường cao BE, CF lần lượt cắt đường tròn tại M và N.
a. Chứng minh: AM = AN
b. Chứng minh: OA vuông góc EF
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Xét tứ giác BCEF có
^CEB = ^CFB = 900
mà 2 góc này kề, cùng nhìn cạnh BC
Vậy tứ giác BCEF là tứ giác nt 1 đường tròn
b, Xét tứ giác AEHF có
^HEA = ^HFA = 900
Vậy tứ giác AEHF là tứ giác nt 1 đường tròn
c, Ta có ^AMN = ^ACN ( góc nt chắn cung AN )
^ANM = ^MBA ( góc nt chắn cung MA )
mà ^ACN = ^MBA ( tứ giác BCEF nt và 2 góc cùng nhìn cung CF )
=> ^AMN = ^ANM Vậy tam giác AMN cân tại A
=> AN = AM
d, Ta có : ^CBM = ^CFE ( góc nt chắn cung CE của tứ giác BCEF )
mặt khác : ^CNM = ^CBM ( góc nt chắn cung CM )
=> ^CFE = ^CNM, mà 2 góc này ở vị trí đồng vị )
=> MN // EF
e, Ta có AO là đường cao tam giác MAN
mà MN // EF ; AO vuông MN => AO vuông EF

a) Xét tứ giác CEHD có:
∠(CED) = 90 0 (do BE là đường cao)
∠(HDC) = 90 0 (do AD là đường cao)
⇒ ∠(CED) + ∠(HDC) = 180 0
Mà ∠(CED) và ∠(HDC) là 2 góc đối của tứ giác CEHD nên CEHD là tứ giác nội tiếp

Lời giải:
a. Tứ giác $BFEC$ có $\widehat{BFC}=\widehat{BEC}=90^0$ và cùng nhìn cạnh $BC$ nên là tgnt
$\Rightarrow \widehat{EBF}=\widehat{ECF}$ (cùng nhìn cạnh $EF$)
$\Leftrightarrow \widehat{ABM}=\widehat{ACN}$
$\Rightarrow \text{sđc(AM)}=\text{sđc(AN)}$
$\Rightarrow AM=AN$
b. Do $AM=AN$ (cmt) nên $\widehat{ABN}=\widehat{ABM}$ (góc nt chắn 2 cung bằng nhau)
hay $\widehat{NBF}=\widehat{HBF}$
hay $BF$ là phân giác $\widehat{NBH}$
Tam giác $BNH$ có $BF$ vừa là đường cao và phân giác nên $BHN$ là tam giác cân
$\Rightarrow BF$ cũng là đường trung tuyến của tam giác
$\Rightarrow F$ là trung điểm NH$
Kẻ tiếp tuyến $Ax$ như hình. Khi đó $Ax\perp AO(1)$
Ta có:
$\widehat{xAB}=\widehat{ACB}$ (theo tc tiếp tuyến)
$\widehat{ACB}=\widehat{AFE}$ (do $BFEC$ là tgnt)
$\Rightarrow \widehat{xAB}=\widehat{AFE}$
Hai góc này ở vị trí so le trong nên $Ax\parallel EF(2)$
Từ $(1); (2)\Rightarrow AO\perp EF$ (đpcm)

A) GÓC BFC=BIC CUNG NHÌN BC DƯỚI MOOTF GÓC=90 \(\Rightarrow\) BCEF NỘI TIẾP
B) VÌ BCEF NỒI TIẾPÓC MBC=CFE
GÓC MNC=MBC(=1/2SĐ CUNG MC)
\(\Rightarrow\) GÓC MNC=CFE\(\Rightarrow\) MN//È
C) VÌ BCEF NỘI TIẾP GÓC FBM=FCE
MÀ FBM=1/2 SĐ CUNG AN , FCE=1/2 SĐ CUNG AM \(\Rightarrow\)CUNG AN=CUNG AM ĐI QUA TRUNG ĐIỂM VUÔNG GÓC È
a: Xét (O) có
góc ACN là góc nội tiếp chắn cung AN
góc ABM là góc nội tiếp chắn cung AM
góc ABM=góc ACN
Do đó: AM=AN
b: Kẻ tiếp tuyến phụ Ax
=>góc xAC=góc ABC
mà góc ABC=góc AEF
nên góc AEF=góc xAC
=>Ax//FE
=>OA vuông góc với FE