
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

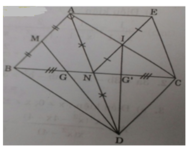
a) Ta có: NB = NC (gt); ND = NA (gt)
⇒ Tứ giác ABDC là hình bình hành
có ∠A = 90o (gt) ⇒ ABDC là hình chữ nhật.
b) Ta có: AI = IC (gt); NI = IE (gt)
⇒ AECN là hình bình hành (hai đường chéo cắt nhau tại trung điểm mỗi đường).
mặt khác ΔABC vuông có AN là trung tuyến nên AN = NC = BC/2.
Vậy tứ giác AECN là hình thoi.
c) BN và DM là 2 đường trung tuyến của tam giác ABD; BN và MD giao nhau tại G nên G là trọng tâm tam giác ABD.
Tương tự G’ là trọng tâm của hai tam giác ACD
⇒ BG = BN/3 và CG’ = CN/3 mà BN = CN (gt) ⇒ BG = CG’
d) Ta có: SABC = (1/2).AB.AC = (1/2).6.6 = 24 (cm2)
Lại có: BG = GG’ = CG’ (tính chất trọng tâm)
⇒ SDGB = SDGG' = SDG'C = 1/3 SBCD
(chung đường cao kẻ từ D và đáy bằng nhau)
Mà SBCD = SCBA (vì ΔBCD = ΔCBA (c.c.c))
⇒SDGG' = 24/3 = 8(cm2)

a: Xét ΔCAB có CF/CA=CE/CB
nên FE//AB và FE=AB/2
=>FE//AD và FE=AD
Xét tứ giác AFED có
FE//AD
FE=AD
góc FAD=90 độ
Do đó: AFED là hình chữ nhật
Xét tứ giác AECK có
F là trung điểm chung của AC và EK
EA=EC
Do đó: AECK là hình thoi
b: \(S_{ABC}=\dfrac{1}{2}\cdot4\cdot5=10\left(cm^2\right)\)

a: Xét ΔCAB có CF/CA=CE/CB
nên FE//AB và FE=AB/2
=>FE//AD và FE=AD
Xét tứ giác AFED có
FE//AD
FE=AD
góc FAD=90 độ
Do đó: AFED là hình chữ nhật
Xét tứ giác AECK có
F là trung điểm chung của AC và EK
EA=EC
Do đó: AECK là hình thoi
b: \(S_{ABC}=\dfrac{1}{2}\cdot4\cdot5=10\left(cm^2\right)\)

Chưa có ai trả lời câu hỏi này, hãy gửi một câu trả lời để giúp tran cong hoai giải bài toán này.
a: Xét tứ giác AEMF có góc AEM=góc AFM=góc FAE=90 độ
nên AEMF là hình chữ nhật
b: AC=8cm
\(S_{ABC}=\dfrac{6\cdot8}{2}=24\left(cm^2\right)\)
c: Đề sai rồi bạn
AM//NB mà
a: Xét tứ giác BECF có
D là trung điểm chung của BC và EF
BE=EC
Do đó: BECF là hình thoi
b: Sửa đề: Tính diện tích BECF
\(BC=\sqrt{10^2-8^2}=6\left(cm\right)\)
DE=AB/2=4cm
=>EF=8cm
\(S_{BECF}=\dfrac{1}{2}\cdot6\cdot8=3\cdot8=24\left(cm^2\right)\)