Nếu \(\left|a\right|=\sqrt{2}\) thì \(\sqrt{a^2}\) lớn hơn só nào sau đây :
| 1,5 | 1,4 | 1,7 | 1,6 |
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
22 tháng 7 2019
Ta thấy tia ló truyền đi sát mặt BC ⇒ góc tới mặt BC bằng góc giới hạn: r2 = igh
Và sin igh = 1/n
Mà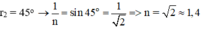 
Đáp án: A
3 tháng 7 2021
a)
\(P=\left(\dfrac{b-a}{\sqrt{b}-\sqrt{a}}-\dfrac{a\sqrt{a}-b\sqrt{b}}{a-b}\right):\dfrac{\left(\sqrt{b}-\sqrt{a}\right)^2+\sqrt{ab}}{\sqrt{a}+\sqrt{b}}\)
\(=\left[\sqrt{b}+\sqrt{a}-\dfrac{\left(\sqrt{a}-\sqrt{b}\right)\left(a+\sqrt{ab}+b\right)}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}\right]:\dfrac{b-\sqrt{ab}+a}{\sqrt{a}+\sqrt{b}}\)
\(=\left(\sqrt{b}+\sqrt{a}-\dfrac{a+\sqrt{ab}+b}{\sqrt{a}+\sqrt{b}}\right).\dfrac{\sqrt{a}+\sqrt{b}}{a-\sqrt{ab}+b}\)
\(=\dfrac{\left(\sqrt{a}+\sqrt{b}\right)^2-a-\sqrt{ab}-b}{\sqrt{a}+\sqrt{b}}.\dfrac{\sqrt{a}+\sqrt{b}}{a-\sqrt{ab}+b}\)
\(=\dfrac{\sqrt{ab}}{\sqrt{a}+\sqrt{b}}.\dfrac{\sqrt{a}+\sqrt{b}}{a-\sqrt{ab}+b}\)\(=\dfrac{\sqrt{ab}}{a-\sqrt{ab}+b}\)
b) \(P=\dfrac{\sqrt{ab}}{a-\sqrt{ab}+b}=\dfrac{\sqrt{ab}}{\left(\sqrt{a}-\dfrac{1}{2}\sqrt{b}\right)^2+\dfrac{3}{4}b}\)
Vì \(\left(\sqrt{a}-\dfrac{1}{2}\sqrt{b}\right)^2+\dfrac{3}{4}b>0;\forall a\ge0;b\ge0;a\ne b\)
\(\sqrt{ab}\ge0\)\(\forall a\ge0;b\ge0\)
\(\Rightarrow P=\dfrac{\sqrt{ab}}{\left(\sqrt{a}-\dfrac{1}{2}\sqrt{b}\right)^2+\dfrac{3}{4}b}\ge0\)
Vậy...
14 tháng 6 2017
với a > 0 và a khác 0. Ta có :
\(\left(\frac{1-a\sqrt{a}}{1-\sqrt{a}}+\sqrt{a}\right)\left(\frac{1-\sqrt{a}}{1-a}\right)^2=1\)
\(\Leftrightarrow\)\(\frac{1-a\sqrt{a}+\sqrt{a}-a}{1-\sqrt{a}}\left(\frac{1-\sqrt{a}}{1-a}\right)^2=1\)
\(\Leftrightarrow\)\(\frac{\sqrt{a}\left(1-a\right)\left(1-a\right)}{1-\sqrt{a}}.\frac{\left(1-\sqrt{a}\right)^2}{\left(1-a\right)^2}=1\)
\(\Leftrightarrow\)\(\frac{\left(1-a\right)\left(1+\sqrt{a}\right).\left(1-\sqrt{a}\right)}{\left(1-a\right)^2}=1\)
\(\Leftrightarrow\)\(\frac{\left(1-a\right)\left(1-a\right)}{\left(1-a\right)^2}=1\)
năm nay em lên lớp 9 anh xem xét bài em nha!!! ^.^
14 tháng 6 2017
Dùng tính chất phân phối
Tách vế trái ra rồi chứng minh :
Tổng vế trái bằng 1
Với a lớn hơn hoặc bằng 0 ; a khác 1 đó là điều kiện để phân thức tồn tại thôi
22 tháng 5 2022
a: \(=4a-4\sqrt{10a}-9\sqrt{10a}=4a-13\sqrt{10a}\)
b: \(=\sqrt{x}\left(4-\sqrt{2}\right)\cdot\sqrt{x}\left(1-\sqrt{2}\right)\)
\(=x\cdot\left(4-4\sqrt{2}-\sqrt{2}+2\right)\)
\(=\left(6-5\sqrt{2}\right)x\)
c: \(=\dfrac{2}{2x-1}\cdot x\sqrt{5}\cdot\left(2x-1\right)=2x\sqrt{5}\)
24 tháng 9 2020
1) \(VT=\frac{\sqrt{a}+\sqrt{b}}{2\left(\sqrt{a}-\sqrt{b}\right)}-\frac{\sqrt{a}-\sqrt{b}}{2\left(\sqrt{a}+\sqrt{b}\right)}+\frac{2b}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}\)
\(=\frac{\left(\sqrt{a}+\sqrt{b}\right)^2-\left(\sqrt{a}-\sqrt{b}\right)^2+4b}{2\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}\)\(=\frac{a+2\sqrt{ab}+b-a+2\sqrt{ab}-b+4b}{2\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}\)
\(=\frac{4\sqrt{ab}+4b}{2\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}\)
\(=\frac{4\sqrt{b}\left(\sqrt{a}+\sqrt{b}\right)}{2\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}=\frac{2\sqrt{b}}{\sqrt{a}-\sqrt{b}}=VP\)(ĐPCM)
2) \(VT=\text{[}\frac{\left(\sqrt{a}+\sqrt{b}\right)\left(a+b-\sqrt{ab}\right)}{\left(\sqrt{a}+\sqrt{b}\right)}-\sqrt{ab}\text{]}.\frac{\left(\sqrt{a}+\sqrt{b}\right)^2}{\left(a-b\right)^2}\)
\(=\frac{\left(a+b-\sqrt{ab}-\sqrt{ab}\right)\left(\sqrt{a}+\sqrt{b}\right)^2}{\left(a-b\right)^2}\)\(=\frac{\left(\sqrt{a}-\sqrt{b}\right)^2\left(\sqrt{a}+\sqrt{b}\right)^2}{\left(a-b\right)^2}=\frac{\left(a-b\right)^2}{\left(a-b\right)^2}=1=VP\)(ĐPCM)
4) \(VT=\left(1+\frac{a+\sqrt{a}}{\sqrt{a}+1}\right)\left(1-\frac{a-\sqrt{a}}{\sqrt{a}-1}\right)\)\(=\left(1+\frac{\sqrt{a}\left(\sqrt{a}+1\right)}{\sqrt{a}+1}\right)\left(1-\frac{\sqrt{a}\left(\sqrt{a}-1\right)}{\sqrt{a}-1}\right)\)
\(=\left(1+\sqrt{a}\right)\left(1-\sqrt{a}\right)=1-a=VP\)(ĐPCM)
LT
25 tháng 6 2021
\(A=\left|2-\sqrt{7}\right|+7-2\sqrt{7}+1\)
\(=\sqrt{7}-2+8-2\sqrt{7}\) \(=6-\sqrt{7}\)
\(B=3\cdot1,5-4\cdot\left|3-\sqrt{2}\right|\) \(=4,5-4\left(3-\sqrt{2}\right)\)
\(=4,5-12+4\sqrt{2}\) \(=4\sqrt{2}-7,5\)
25 tháng 6 2021
Ta có: \(A=\sqrt{\left(2-\sqrt{7}\right)^2}+\left(\sqrt{7}-1\right)^2\)
\(=\sqrt{7}-2+8-2\sqrt{7}\)
\(=6-\sqrt{7}\)
1,4