Cho góc a với tanα=\(\dfrac{-3}{4}\). Tính giá trị của cosα
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 10 2021
a: \(\cos\alpha=\dfrac{1}{2}\)
\(\tan\alpha=\sqrt{3}\)
\(\cot\alpha=\dfrac{\sqrt{3}}{3}\)
6 tháng 11 2021
Có sin2a + cos2a = 1
Mà cos a = \(\dfrac{3}{4}\)
=> sin2a + (\(\dfrac{3}{4}\))2 = 1
=> sin2a + \(\dfrac{3^2}{4^2}\) = 1
=> sin2a + \(\dfrac{9}{16}\)= 1
=> sin2a = \(\dfrac{7}{16}\)
=> sin a = \(\dfrac{\sqrt{7}}{4}\)
Có tan a = \(\dfrac{\text{sin a}}{\text{cos a}}\)
Mà \(\left\{{}\begin{matrix}\text{cos a = }\dfrac{3}{4}\\\text{sin a = }\dfrac{\sqrt{7}}{4}\end{matrix}\right.\)
=> tan a = \(\dfrac{\dfrac{\sqrt{7}}{4}}{\dfrac{3}{4}}\) = \(\dfrac{\sqrt{7}}{4}\): \(\dfrac{3}{4}\) = \(\dfrac{\sqrt{7}}{4}\).\(\dfrac{4}{3}\) =\(\dfrac{\sqrt{7}}{3}\)
DN
1
18 tháng 1 2022
Vì \(\dfrac{\pi}{2}< \alpha< \pi\) \(\Rightarrow\) cos \(\alpha\) < 0
\(\Rightarrow\) cos \(\alpha\) = \(-\sqrt{1-sin^2\alpha}\) = \(-\dfrac{2\sqrt{2}}{3}\)
\(\Rightarrow\) tan \(\alpha\) = \(\dfrac{sin\alpha}{cos\alpha}=\dfrac{-\sqrt{2}}{4}\)
\(\Rightarrow\) cot \(\alpha\) = \(\dfrac{1}{tan\alpha}\) = \(-2\sqrt{2}\)
Chúc bn học tốt!
CM
28 tháng 9 2018
a, Tìm được sinα = 24 5 , tanα = 24 , cotα = 1 24
b, cosα = 5 3 , tanα = 2 5 , cotα = 5 2
c, sinα = ± 2 5 , cosα = ± 1 5 , cotα = 1 2
d, sinα = ± 1 10 , cosα = ± 3 10 , tanα = 1 3
TC
1
F
7 tháng 4 2022
Em 2k8 ms học nên k chắc
Vì 0 < \(\alpha< \dfrac{\pi}{2}\) => sin \(\alpha>0\)
Cos \(\alpha=\dfrac{1}{3}\) \(\Rightarrow sin\alpha=\sqrt{1-\dfrac{1}{9}}=\dfrac{2\sqrt{2}}{3}\)
tan \(\alpha=2\sqrt{2}\) ; cot \(\alpha=\dfrac{1}{2\sqrt{2}}\)
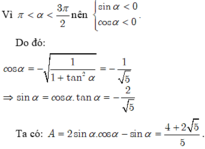
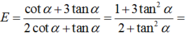
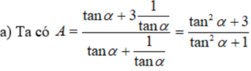
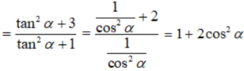
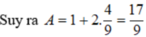
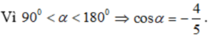
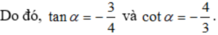
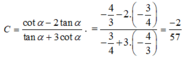
1+tan^2a=1/cos^2a
=>1/cos^2a=1+9/16=25/16
=>cos^2a=16/25
=>cosa=4/5 hoặc cosa=-4/5