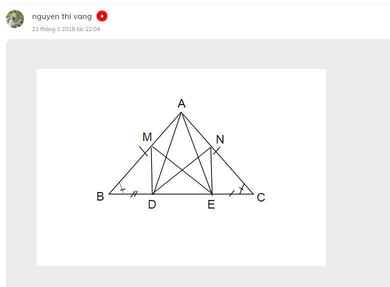
Cho tam giác ABC vuông cân tại A, từ A kẻ đường thẳng d nằm ngoài tam giác ABC, kẻ BD vuông góc với d, CE cũng vuông góc với d; gọi M là TĐ của BC. CMR tam giác MDE vuông cân.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 1 2016
Ta có Â 1 + Â 2 + Â 3 = 180 độ
Mà Â 2 = 90 độ
Suy ra  1 +  2 = 90 độ
Tam giác vuông ABD có :
Â1 + C^ = 90 độ
Mà Â 1 + Â 3 = 90 độ
Suy ra  3 = góc ACE
Xét tam giác BDA tam giác AEC có :
BA = CA ( GIẢ THIẾT )
Góc DAB = Góc ECA ( CHỨNG MINH TRÊN )
Suy ra tam giác BDA = tam giác AEC(ạnh huyền -góc nhọn )
Suy ra AE = BD (2 cạnh tương ứng )
AD = CE ( 2 cạnh tương ứng )
ta có DE = AE + AD
Suy ra DE = BD + CE
Mà
25 tháng 8 2017
2. Cho tam giác ABC vuông cân tại A.. Qua A vẽ đường thẳng d ở ngoài tam giác ABC . Vẽ BD vuông góc với d taị D. CE vuông góc với d tại E. M là trung điểm CB. Chứng minh rằng:
a) BD + CE = DE
b) Tam giác MDE là tam giác vuông cân
KV
5 tháng 5 2023
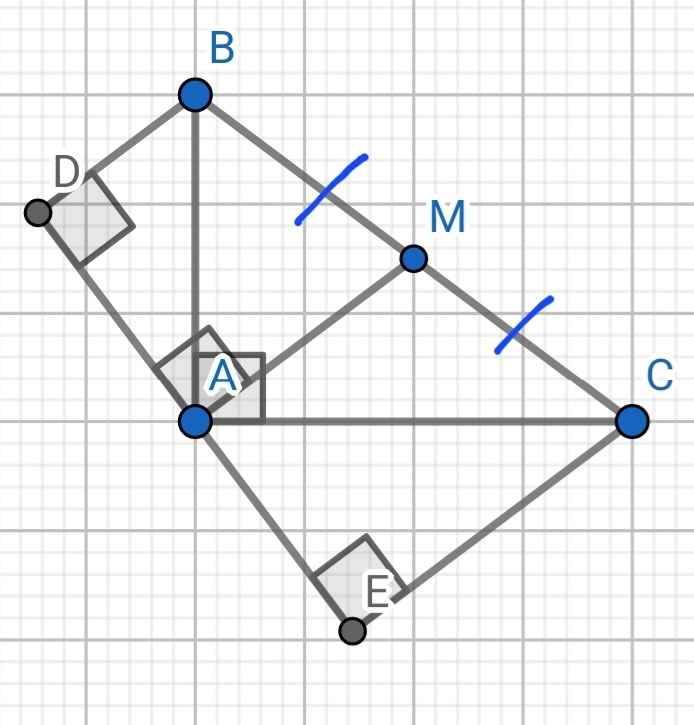
a) Sửa đề: Chứng minh ∆ABC ∽ ∆EAC
Giải:
∆ABC vuông tại A
⇒ BC² = AB² + AC² (Pytago)
= 6² + 8²
= 100
⇒ BC = 10 (cm)
Do AM là đường trung tuyến ứng với cạnh huyền BC
⇒ AM = BM = CM = BC : 2
= 10 : 2 = 5 (cm)
∆AMC có AM = CM = 5 (cm)
⇒ ∆AMC cân tại M
⇒ ∠MAC = ∠MCA (hai góc ở đáy)
Do MA ⊥ DE (gt)
CE ⊥ DE (gt)
⇒ MA // DE
⇒ ∠MAC = ∠ACE (so le trong)
Mà ∠MAC = ∠MCA (cmt)
⇒ ∠MAC = ∠ACE
⇒ ∠ACE = ∠BCA (do ∠MAC = ∠BAC)
Xét hai tam giác vuông:
∆ABC và ∆EAC có:
∠BCA = ∠ACE (cmt)
⇒ ∆ABC ∽ ∆EAC (g-g)
b) Do ∆ABC ∽ ∆EAC (cmt)
⇒ AC/CE = BC/AC
⇒ CE = AC²/BC
= 8²/10
= 6,4 (cm)
