Mọi người giup em với, cần gấp lời giải ah !!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔCDA vuông tại A và ΔCBA vuông tại A có
CA chug
DA=BA
Do đó:ΔCDA=ΔCBA
b: Ta có: ΔCDB cân tại C
mà CA là đường cao
nên CA là đường phân giác
c: Xét ΔCEI vuông tại E và ΔCFI vuôg tại F có
CI chung
\(\widehat{ECI}=\widehat{FCI}\)
Do đó:ΔCEI=ΔCFI
Suy ra: CE=CF
Xét ΔCDB có CE/CD=CF/CB
nên EF//DB

a: Thay x=0 và y=5 vào (d), ta được:
m*0+5=5
=>5=5(đúng)
=>ĐPCM
b: x1<x2; |x1|>|x2|
=>x1*x2<0
PTHĐGĐ là:
x^2-mx-5=0
Vì a*c<0
nên x1,x2 luôn trái dấu
=>Với mọi m

-Bài 3:
2) -Áp dụng BĐT Caushy Schwarz ta có:
\(A=\dfrac{1}{x^3+3xy^2}+\dfrac{1}{y^3+3x^2y}\ge\dfrac{\left(1+1\right)^2}{x^3+3xy^2+3x^2y+y^3}=\dfrac{4}{\left(x+y\right)^3}\ge\dfrac{4}{1^3}=4\)-Dấu "=" xảy ra khi \(x=y=\dfrac{1}{2}\)

vẽ lại mạch ta có RAM//RMN//RNB
đặt theo thứ tự 3 R là a,b,c
ta có a+b+c=1 (1)
điện trở tương đương \(\dfrac{1}{R_{td}}=\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\) \(\Rightarrow I=\dfrac{U}{R_{td}}=9.\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\) với a,b,c>0
áp dụng bất đẳng thức cô si cho \(\dfrac{1}{a},\dfrac{1}{b},\dfrac{1}{c}\) \(\Rightarrow\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge\dfrac{3}{\sqrt[3]{abc}}\ge\dfrac{3}{\left(\dfrac{a+b+c}{3}\right)}=\dfrac{9}{a+b+c}=9\)
\(\Leftrightarrow9\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\ge81\Leftrightarrow I\ge81\) I min =81 ( úi dồi ôi O_o hơi to mà vẫn đúng đá nhỉ)
dấu ''='' xảy ra \(\Leftrightarrow a=b=c\left(2\right)\)
từ (1) (2) \(\Rightarrow a=b=c=\dfrac{1}{3}\left(\Omega\right)\)
vậy ... (V LUN MẤT CẢ BUỔI TỐI R BÀI KHÓ QUÁ EM ĐANG ÔN HSG À )

3:
a:Các tia trên hình là Ax,Ay,Bx,By,Cx,Cy
=>Có 6 tia
b: AB<AC
=>B nằm giữa A và C
=>AB+BC=AC
=>BC=4cm
c: AI=3/2=1,5cm
CI=7-1,5=5,5cm

Câu 3:
a)
CTPT xủa X là CnH2n+2O
\(n_{CO_2}=\dfrac{8,96}{22,4}=0,4\left(mol\right)\Rightarrow n_{C_nH_{2n+2}O}=\dfrac{0,4}{n}\left(mol\right)\)
=> \(n_{H_2O}=\dfrac{\dfrac{0,4}{n}.\left(2n+2\right)}{2}=\dfrac{0,4}{n}\left(n+1\right)\left(mol\right)\)
Mà \(n_{H_2O}=\dfrac{9}{18}=0,5\left(mol\right)\)
=> n = 4
=> CTPT: C4H10O
b) \(n_{C_4H_{10}O}=\dfrac{0,4}{4}=0,1\left(mol\right)\)
=> m = 0,1.74 = 7,4 (g)
c)
(1) \(CH_3-CH_2-CH_2-CH_2OH\)
(2) \(CH_3-CH_2-CH\left(OH\right)-CH_3\)
(3) \(CH_3-C\left(CH_3\right)\left(OH\right)-CH_3\)
(4) \(CH_3-CH\left(CH_3\right)-CH_2OH\)
(5) \(CH_3-CH_2-CH_2-O-CH_3\)
(6) \(CH_3-CH\left(CH_3\right)-O-CH_3\)
(7) \(CH_3-CH_2-O-CH_2-CH_3\)
d)
X là \(CH_3-C\left(CH_3\right)\left(OH\right)-CH_3\) (2-metylpropan-2-ol)

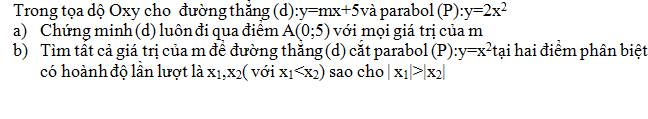



 mọi người giúp em với ạ em đang cần gấp!!
mọi người giúp em với ạ em đang cần gấp!!
a.
\(A\in Z\Rightarrow2A\in Z\Rightarrow\dfrac{2\left(3x-2\right)}{2x-3}\in Z\)
\(\Rightarrow\dfrac{6x-4}{2x-3}\in Z\Rightarrow\dfrac{3\left(2x-3\right)+5}{2x-3}\in Z\)
\(\Rightarrow3+\dfrac{5}{2x-3}\in Z\Rightarrow\dfrac{5}{2x-3}\in Z\)
\(\Rightarrow2x-3=Ư\left(5\right)=\left\{-5;-1;1;5\right\}\)
\(\Rightarrow x=\left\{-1;1;2;4\right\}\)
Thử lại thấy đều thỏa mãn
b.
\(\dfrac{2x+4}{y}-\dfrac{2}{x}-\dfrac{5}{xy}=1\)
\(\Rightarrow x\left(2x+4\right)-2y-5=xy\)
\(\Leftrightarrow2x^2+4x-y-5=xy\)
\(\Leftrightarrow2x^2+4x-5=y\left(x+1\right)\)
Với \(x=-1\) không thỏa mãn
Với \(x\ne-1\Rightarrow y=\dfrac{2x^2+4x-5}{x+1}\) (1)
Do \(y\in Z\Rightarrow\dfrac{2x^2+4x-5}{x+1}\in Z\Rightarrow\dfrac{2x^2+4x+2-7}{x+1}\in Z\)
\(\Rightarrow\dfrac{2\left(x+1\right)^2-7}{x+1}\in Z\Rightarrow2\left(x+1\right)-\dfrac{7}{x+1}\in Z\)
\(\Rightarrow\dfrac{7}{x+1}\in Z\) do \(2\left(x+1\right)\in Z\) với \(x\in Z\)
\(\Rightarrow x+1=Ư\left(7\right)=\left\{-7;-1;1;7\right\}\)
\(\Rightarrow\left[{}\begin{matrix}x=-8\left(loại\right)\\x=-2\left(loại\right)\\x=0\\x=6\end{matrix}\right.\)
Thế vào (1): \(\left[{}\begin{matrix}x=0\Rightarrow y=-5< 0\left(loại\right)\\x=6\Rightarrow y=13\end{matrix}\right.\)
Vậy \(\left(x;y\right)=\left(6;13\right)\)