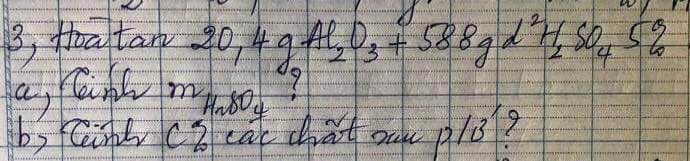Mọi người cho mình xin nguyên lí hoạt động của tắc te với chấn lưu với ạ. Mình cảm ơn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LV
0
H
5 tháng 4 2021
Để làm dạng này , bạn làm như sau :
Vì bạn biết 1 giờ = 60 phút; 1 phút =60 giây nên là
Trước hết bạn lấy số 0,8325 (số chỉ giờ) nhân 60 nhé = 49,95
Bạn lấy phần nguyên của nó trước dấu phẩy là 49 , điền vảo chỗ chấm trước phút.
Cái phần thập phân sau dấu phẩy là 0,95 bạn tiếp tục nhân 60 = 57.
Bạn điền 57 vào phần chỗ chấm trước giây.
Vậy 0,8325 giờ=49 phút 57 giây
HT
1
19 tháng 8 2021
PTHH: \(Al_2O_3+3H_2SO_4\rightarrow Al_2\left(SO_4\right)_3+3H_2O\)
Ta có: \(\left\{{}\begin{matrix}m_{H_2SO_4}=588\cdot5\%=29,4\left(g\right)\Rightarrow n_{H_2SO_4}=\dfrac{29,4}{98}=0,3\left(mol\right)\\n_{Al_2O_3}=\dfrac{20,4}{102}=0,2\left(mol\right)\end{matrix}\right.\)
Xét tỉ lệ: \(\dfrac{0,2}{1}>\dfrac{0,3}{3}\) \(\Rightarrow\) Al2O3 còn dư
\(\Rightarrow n_{Al_2\left(SO_4\right)_3}=0,1\left(mol\right)=n_{Al_2O_3\left(dư\right)}\)
\(\Rightarrow C\%_{Al_2\left(SO_4\right)_3}=\dfrac{0,1\cdot342}{20,4+588-0,1\cdot102}\cdot100\%\approx5,72\%\)
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 1 2022
Hàm bậc 2 có \(\left\{{}\begin{matrix}a=1>0\\-\dfrac{b}{2a}=6-m\end{matrix}\right.\) nên nghịch biến trên khoảng \(\left(-\infty;6-m\right)\)
Hàm nghịch biến trên khoảng đã cho khi:
\(6-m\ge2\Rightarrow m\le4\)
\(\Rightarrow\) Có 4 giá trị nguyên dương của m
