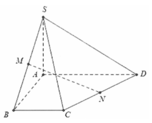
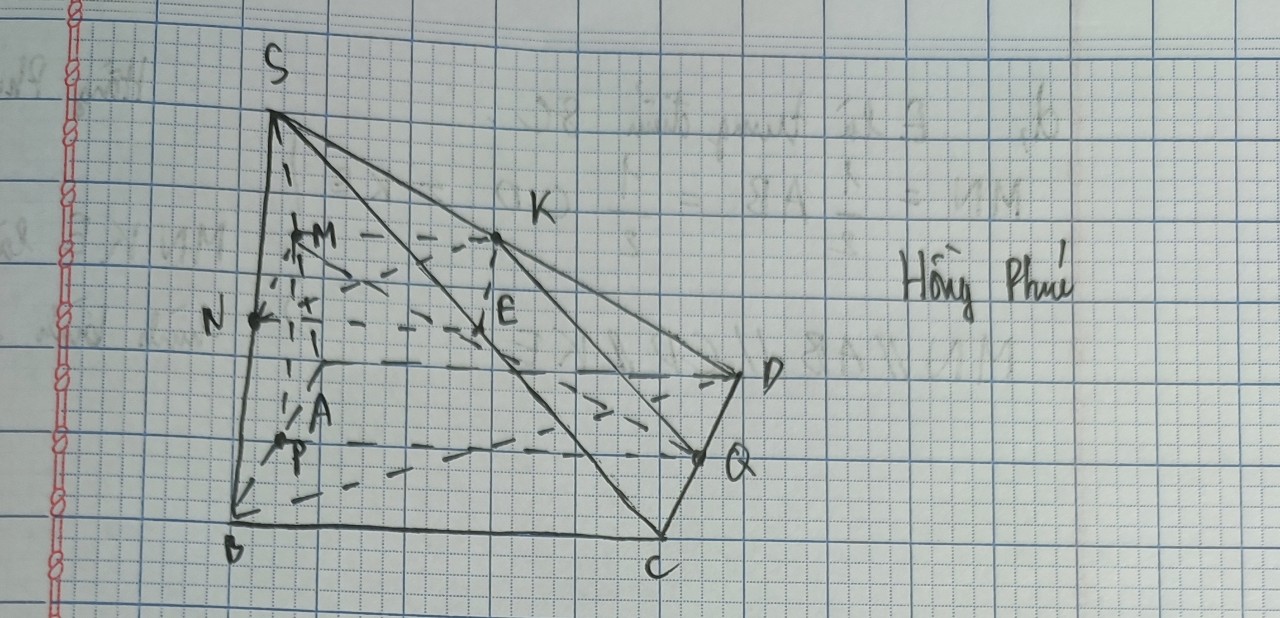
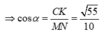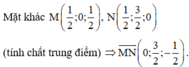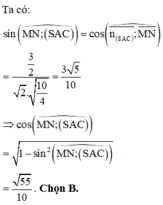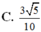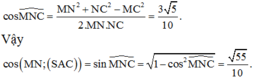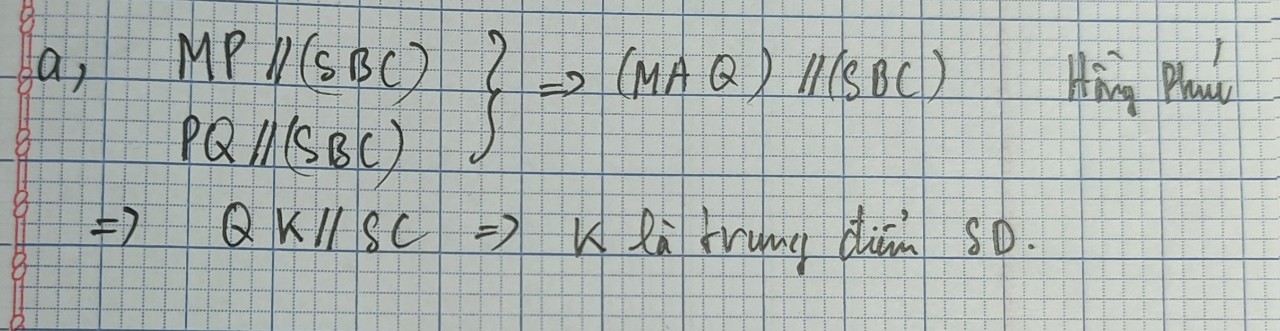Cho hình chóp S.ABCD, ABCD là hình thang, đáy lớn AD=2BC. Gọi M, N lần lượt là trung điểm của AD, CD. a/. Chứng minh: MN//(SAC). b/. Gọi K SB sao cho KB 2KS . Xác định giao điểm của đường thẳng SA và (MNK). c/. Gọi G là trọng tâm tam giác CDM. Chứng minh KG//SD.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
4 tháng 5 2019
Chọn C
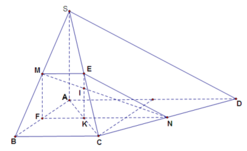
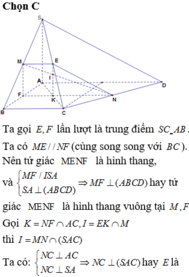
Ta gọi E, F lần lượt là trung điểm của SC, AB
Ta có ME//NF(do cùng song song với BC. Nên tứ giác MENF là hình thang, và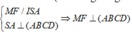 
hay tứ giác MENF là hình thang vuông tại M, F
Ta có: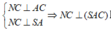 
hay E là hình chiếu vuông góc của N lên (SAC)
Từ đó ta có được, góc giữa MN và (SAC) là góc giữa MN và CI
Suy ra, gọi
α
là góc giữa MN và (SAC) thì 
CM
3 tháng 7 2018
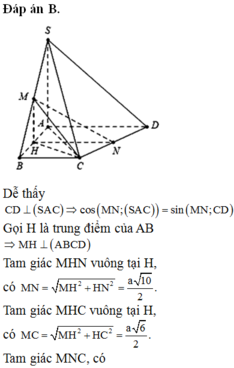
Đáp án B
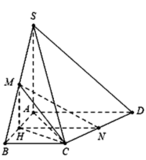
Dễ thấy 
Gọi H là trung điểm của AB 
Tam giác MHN vuông tại H, có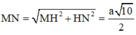 
Tam giác MHC vuông tại H, có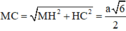 
Tam giác MNC, có
c
o
s
M
N
C
^
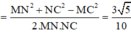
Vậy cos(MN;(SAC)) = sin M N C ^ = 1 - cos 2 M N C ^ = 55 10
CM
9 tháng 10 2018
Đáp án C
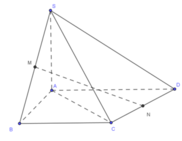
Kẻ CN
⊥
AB ta dễ dàng tính được 
=> tam giác ADC vuông tại C. Từ đó NC ⊥ (SAC)
Gọi O là trung điểm của AC, dễ dàng cm được BD ⊥ (SAC)
=> MK ⊥ (SAC). vơí K là trung điểm của SO, từ đó KC là hc của MN lên .
Ta kẻ KZ ⊥ AC
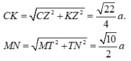
với T là trung điểm của AB.
Gọi α là góc tạo với MN và (SAC)
