Cho Δ ABC vuông ở A(AB<AC), đường cao AH (HϵBC). gọi D là điểm đối xứng với A qua H.Lấy điểm E đối xứng với B qua AD
a) Chứng minh tứ giác ABDE là hình thoi
b) Chứng minh AE \(\perp\) DC
c) Gọi I là trung điểm của EC; F là giao điểm của AE và DC. Tính diện tích ΔHFI biết AD=8cm; EC=6cm

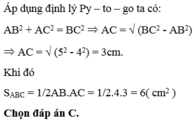
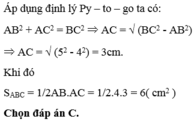
a: Xét ΔBAD có
BH vừa là đường cao, vừa là trung tuyến
nên ΔBAD cân tại B
E đối xứng với B qua AD
nên AE=AB; DE=DB
mà BA=BD
nên AE=AB=DE=DB
=>ABDE là hình thoi
b: Vì ABDE là hình thoi
nên AB//DE
=>DE vuông góc với AC
Xét ΔCDA có
DE,CH là các đường cao
DE cắt CH tại E
Do đó: E là trực tâm
=>AE vuông góc với CD