giúp mình với chiều mình phải nộp rồi. Cảm ơn nhìu
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HA
Giúp mình nka:3 chiều mình phải nộp gòi, cảm ơn các bạn nhìu nhắm<3
1
DN
4
25 tháng 2 2023
(っ◔◡◔)っ ♥ Aurora ♥giúp tui với bạn ơi cảm ơn bạn nhìu nha 
DG
Làm ơn giúp mình với chiều nay mình phải nộp rồi cảm ơn nhé
Ko nhìn thấy thì ấn vào rồi phóng to lên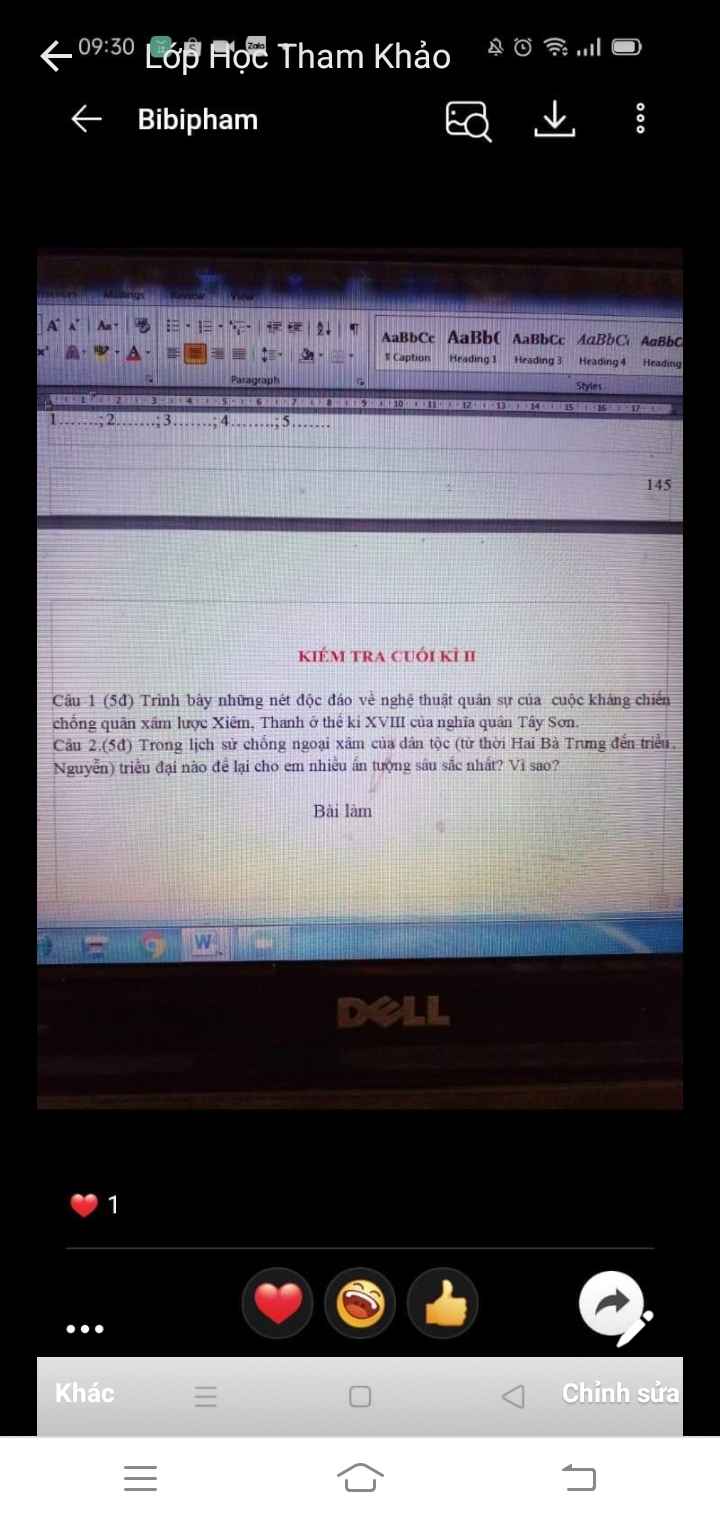
1
KD
13 tháng 5 2021
Câu 1
Trước hết, Nguyễn Huệ và Bộ Chỉ huy quân Tây Sơn đã triệt để lợi dụng địa hình thiên hiểm, bí mật tạo lập thế trận hiểm hóc đánh địch
+) Thứ hai, thực hiện mưu kế “điệu hổ ly sơn” dẫn dắt chúng vào nơi ta chuẩn bị để tiêu diệt
Câu 2
Em thích nhất triều đại nhà Ngô( 939-965 )
Vì: Em thích Ngô Quyền trong cách đánh chủ động và độc đáo
13 tháng 5 2021
Bạn ơi câu 1 là thế kỉ 17 mà
Câu 2 bạn có thể viết dài hơn đc ko ạ
YN
2
H
28 tháng 4 2022
1)
a. Xét tg ABC cân tại A có AC=AB; gACB = g ABC.
Xét tg ACN và tg ABM có:
CN=BM (gt)
AC=AB
gACB=gABC
=> tg ACN = tg ABM (cgc)
=> AN=AM (2 cạnh tg ứng)
H là trung điểm BC nên AH là đường trung tuyến của tg ABC
Mak tg ABC cân => H cũng là đường cao của tg ABC => AH ⊥ BC
b. Vì H là trung đ của BC nên CH=HB=BC/2= 3cm
Áp dụng định lý Py ta go vào tg AHB có:
AB^2=AH^2+HB^2
AH^2= AB^2 - HB^2
AH^2= 5^2 - 3^2 = 16 cm
=> AH= 4 cm
c. Xét tg AMN và tg KMB có:
AM=KM (gt)
MN=BM (gt)
gHMA=gKMB (đối đỉnh)
=> tg AMN = tg KMB (cgc)
d. tg AMN = tg KMB => gMAN=gMKB
=> AN=KB=Am
Mà AB>AM (quan hệ giữ đường xiêng và hình chiếu) nên AB>BK
=> gBKA> gBAK
=> gMAN>gBAM
HT
2
15 tháng 12 2021
a. Chu vi là \(\left(12+5\right).2=34\left(m\right)\)
Diện tích là \(12.5=60\left(m^2\right)=600000\left(cm^2\right)\)
b. Cần lát \(600000:\left(40.40\right)=375\) viên gạch
HT
7
giúp mình với ,ngày mai mình phải nộp rồi, cảm ơn
AH
Akai Haruma
Giáo viên
21 tháng 9 2021
Lời giải:
Hình 1:
Ta thấy $\widehat{xAB}=\widehat{ABy}=120^0$, mà 2 góc này ở vị trí so le trong nên $Ax\parallel By(1)$
Lại có:
$\widehat{ABy}+\widehat{yBC}+\widehat{ABC}=360^0$
$120^0+\widehat{yBC}+80^0=360^0$
$\widehat{yBC}=160^0$
Vậy: $\widehat{yBC}=\widehat{BCz}=160^0$. Mà hai góc này ở vị trí so le trong nên $By\parallel Cz(2)$
Từ $(1);(2)\Rightarrow Ax\parallel By\parallel Cz$
----------------------
Hình 2:
$\widehat{xAB}+\widehat{ABy}=65^0+115^0=180^0$, mà 2 góc này ở vị trí trong cùng phía nên $Ax\parallel By(1)$
$\widehat{CBy}+\widehat{BCz}=130^0+50^0=180^0$, mà 2 góc này ở vị trí trong cùng phía nên $By\parallel Cz(2)$
Từ $(1);(2)\Rightarrow Ax\parallel By\parallel Cz$
