câu 12 cho tam giác ABC điểm D thuộc cạnh BC.Từ điểm D vẽ DE song song với AD sao cho E thuộc cạnh AC,vẽ DF//AC sao cho điểm F thuộc AB chứng minh tứ giác AEDF là hình bình hành.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 11 2021
a: Xét tứ giác AEDF có
AE//DF
DE//AF
Do đó: AEDF là hình bình hành
mà \(\widehat{DAE}=90^0\)
nên AEDF là hình chữ nhật
13 tháng 11 2021
a, Vì DE//AB nên DE⊥AC và DF//AC nên DF⊥AB
Vì \(\widehat{AED}=\widehat{AFD}=\widehat{EAF}=90^0\) nên AEDF là hcn
b,Vì E là trung điểm MD và AC nên AMCD là hbh
Mà AC⊥DE nên AMCD là hthoi
c, Vì D là trung điểm BC và AK và \(\widehat{BAC}=90^0\) nên ABKC là hcn
Để ABKC là hv thì AB=AC hay tam giác ABC vuông cân tại A
5 tháng 11 2021
a: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
Do đó: AEDF là hình chữ nhật
31 tháng 10 2021
Xét tứ giác AEDF có
AE//DF
DE//AF
Do đó: AEDF là hình bình hành
mà \(\widehat{DAE}=90^0\)
nên AEDF là hình chữ nhật
16 tháng 10 2018
Ta có: EF // BD (gt)
BF // ED (gt)
Suy ra EF = BD; BF = DE (t/c đoạn chắn)
Trên AB lấy K sao cho AF = BK
ΔAFEΔAFE và ΔKBDΔKBD có:
AF = BK (cách vẽ)
AFE = KBD (đồng vị)
EF = BD (cmt)
Do đó, ΔAFE=ΔKBD(c.g.c)ΔAFE=ΔKBD(c.g.c)
=> AE = KD (2 cạnh t/ứ)
= BF = ED (theo gt AE = BF, theo cmt BF = ED)
Kẻ DM⊥AB;DN⊥ACDM⊥AB;DN⊥AC
ΔΔ DMK vuông tại M và ΔΔ DNE vuông tại N có:
DK = DE (cmt)
MKD = NED (cùng đồng vị với FAE)
Do đó, ΔDMK=ΔDNEΔDMK=ΔDNE (cạnh huyền - góc nhọn)
=> DM = DN (2 cạnh t/ứ)
=> D cách đều AB và AC (đpcm)
thông cảm nha mk llafm vội nên ko để ý nên ko chác chắn bài
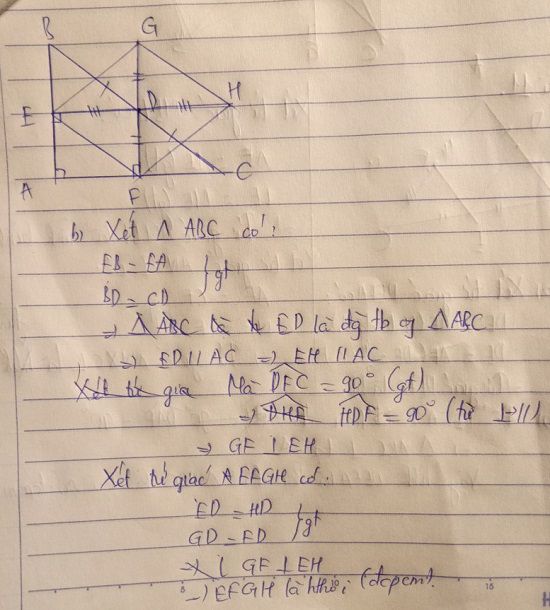
Xét tứ giác AEDF có
AE//DF
AF//DE
Do đó: AEDF là hình bình hành