Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a/ Ta có: O là giao điểm 2 đường chéo (gt) => O là trung điểm của AC và BD => BO = OD
Xét tg DOM và tg BON ta có: BO = OD (cmt); \(\widehat{DOM}=\widehat{BON}\) ( đối đỉnh); \(\widehat{ODM}=\widehat{OBN}\)( so le trong)
=> tg DOM = tg BON (g.c.g) =>> DM = BN
b/ Ta có: AD // BC (vì ABCD là hình vuông) ma M \(\in\)AD va N \(\in\) BC
=> MD // BN mà MD = BN (cmt) =>. Tứ giác BMDN là hình bình hành
Câu 3:
Xét ΔMDC có AB//CD
nên MA/MD=MB/MC(1)
Xét ΔMDK có AI//DK
nên AI/DK=MA/MD(2)
Xét ΔMKC có IB//KC
nên IB/KC=MB/MC(3)
Từ (1), (2) và (3) suy ra AI/DK=IB/KC=MI/MK
Vì AI//KC nên AI/KC=NI/NK=NA/NC
Vì IB//DK nên IB/DK=NI/NK
=>AI/KC=IB/DK
mà AI/DK=IB/KC
nên \(\dfrac{AI}{KC}\cdot\dfrac{AI}{DK}=\dfrac{IB}{DK}\cdot\dfrac{IB}{DC}\)
=>AI=IB
=>I là trung điểm của AB
AI/DK=BI/KC
mà AI=BI
nên DK=KC
hay K là trung điểm của CD
Đặt cạnh hình vuông là a, ta có \(BD=\sqrt{a^2+a^2}=a\sqrt{2}\)
\(\Rightarrow BO=\dfrac{1}{2}BD=\dfrac{a\sqrt{2}}{2}\Rightarrow BO.BD=a^2\)
Xét 2 tam giác vuông AED và MAB có:
\(\left\{{}\begin{matrix}\widehat{ADE}=\widehat{MBA}=90^0\\\widehat{AED}=\widehat{MAB}\left(slt\right)\end{matrix}\right.\) \(\Rightarrow\Delta AED\sim\Delta MAB\left(g.g\right)\)
\(\Rightarrow\dfrac{AD}{BM}=\dfrac{ED}{AB}\Rightarrow BM.ED=AD.AB=a^2\)
\(\Rightarrow BM.ED=BO.BD\)
Mà \(ED=BF\) (do \(BC=CD\) và \(CE=CF\))
\(\Rightarrow BM.BF=BO.BD\Rightarrow\dfrac{BM}{BD}=\dfrac{BO}{BF}\)
Xét hai tam giác BOM và BFD có:
\(\left\{{}\begin{matrix}\dfrac{BM}{BD}=\dfrac{BO}{BF}\\\widehat{OBM}\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta BOM\sim\Delta BFD\left(c.g.c\right)\)
△AOE và △BOG có:
\(AO=BO\) (O là tâm hình vuông ABCD).
\(AE=BG\)
\(\widehat{OAE}=\widehat{OBG}=45^0\)
\(\Rightarrow\)△AOE=△BOG (c-g-c).
\(\Rightarrow OE=OG;\widehat{AOE}=\widehat{BOG}\)
Mà \(\widehat{AOE}+\widehat{BOE}=90^0\) \(\Rightarrow\widehat{GOE}=\widehat{BOG}+\widehat{BOE}=90^0\)
\(\Rightarrow\)△OGE vuông cân tại O.
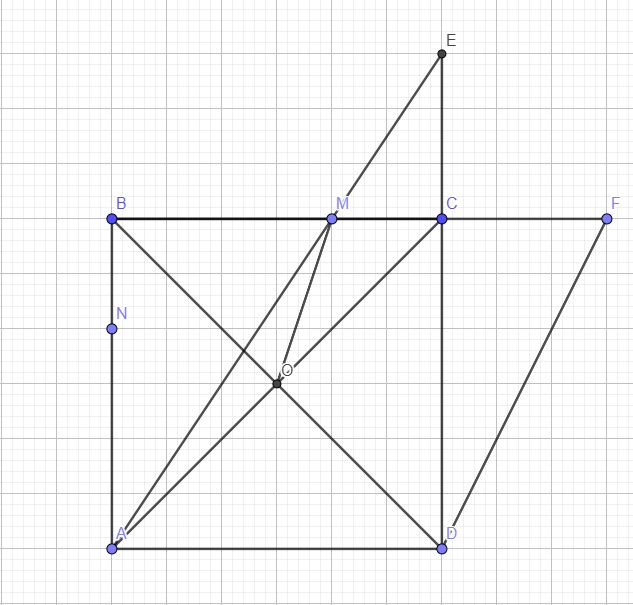
a: Xét ΔDOM và ΔBON có
góc DOM=góc BON
OD=OB
góc ODM=góc OBN
=>ΔDOM=ΔBON
=>DM=BN
mà DM//BN
nên BMDN là hình bình hành
b: Xét ΔEAM vuông tại A và ΔNBE vuông tại B có
EA=NB
AM=BE
Do đó: ΔEAM=ΔNBE
=>EM=EN
=>ΔEMN cân tại E
mà EO là trung tuyến
nen EO vuông góc với MN