Cho hình chóp S.ABCD. ABCD là hình bình hành tâm O.Gọi K, H là trung điểm SB, BD a) (SBD) giao với (SAC) = ? (SAC) giao với (KHC) = ? b) Xác định giao điểm I của SA giao với ( KHC) Xác định thiết diện của hình chóp cắt (KHC) c) Xác định giao điểm E của AB giao với ( KHC) d) Xác định giao điểm F của AD giao với (KHC) e) Tính SI/SA = ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
1 tháng 2 2019
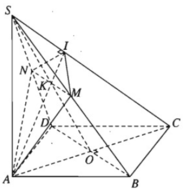
a) Gọi I là giao điểm của mặt phẳng (α) với cạnh SC. Ta có: (α) ⊥ SC, AI ⊂ (α) ⇒ SC ⊥ AI. Vậy AI là đường cao của tam giác vuông SAC. Trong mặt phẳng (SAC), đường cao AI cắt SO tại K và AI ⊂ (α), nên K là giao điểm của SO với (α).
b) Ta có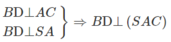 
⇒ BD ⊥ SC
Mặt khác BD ⊂ (SBD) nên (SBD) ⊥ (SAC).
Vì BD ⊥ SC và (α) ⊥ SC nhưng BD không chứa trong (α) nên BD // (α)
Ta có K = SO ∩ (α) và SO thuộc mặt phẳng (SBD) nên K là một điểm chung của (α) và (SBD).
Mặt phẳng (SBD) chứa BD // (α) nên cắt theo giao tuyến d // BD. Giao tuyến này đi qua K là điểm chung của (α) và (SBD).
Gọi M và N lần lượt là giao điểm của d với SB và SD. Ta được thiết diện là tứ giác AIMN vuông góc với SC và đường chéo MN song song với BD.
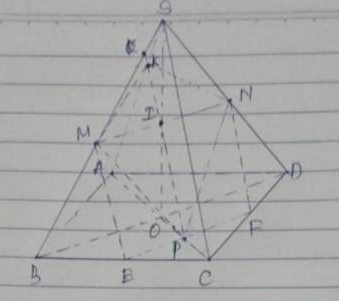
a: BD giao AC tại O
S thuộc (SBD) giao (SAC)
=>(SBD) giao (SAC)=SO
Gọi giao của SO và KH là G
\(\left\{{}\begin{matrix}G\in KH\subset\left(KHC\right)\\G\in SO\subset\left(SAC\right)\end{matrix}\right.\)
\(\left\{{}\begin{matrix}C\in\left(KHC\right)\\C\in\left(SAC\right)\end{matrix}\right.\)
=>(KHC) giao (SAC)=CG
b: Chọn mp (SAC) có chứa SA
(SAC) giao (KHC)=CG
=>I=SA giao CG
c: Chọn mp (ABCD) có chứa AB
(ABCD) cắt (KHC)=HC
=>E=AB giao HC