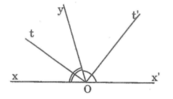
cho tia Ot và tia Ot' lần lượt là tia phân giác của hai góc kề bù xOy và yOx' . Tính số đo của góc tOt'
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Mình có làm bài tương tự khác mỗi số. Bạn chịu khó tìm nhé. Làm lại lười lắm.

Em tự vẽ hình nha
Giải
Có xOy và yOx' là 2 góc kề bù
=> xOy+yOx'=180 độ
Thay số : 100 độ+ yOx'=180 độ
=> yOx'=80 độ
Có tia Ot là phân giác của xOy
=>xOt=tOy=100 độ / 2= 50 độ
Có tia Ot' là phân giác của x'Oy
=>x'Ot'=t'Oy=80 độ / 2 = 40 độ
Có xOt' và x'Ot' là 2 góc kề bù
=> xOt'+x'Ot'=180 độ
Thay số: xOt'+40 độ = 180 độ
=> xOt'=140 độ
Có xOt và x'Ot là 2 góc kề bù
=>xOt+x'Ot=180 độ
Thay số: 50 độ+x'Ot=180 độ
=>x'Ot=130 độ
Trên cùng một nửa mặt phẳng bờ chứa tia Ox có xOt<xOt' ( 50 độ < 140 độ)
=> Tia Ot nằm giữa tia Ox và tia Ot'
=>xOt+tOt'=xOt'
Thay số: 50 độ+tOt'=140 độ
=>tOt'=90 độ
Khi làm bài em nhớ ghi thêm kí hiệu góc, trên olm anh ko biết ghi thế nào

không có số đo cụ thể k tính đc chỉ có góc tot; là 90 độ thôi
xOy+yOx'=180
xOt+tOy+yOt'+t'Ox'=180
2 x tOy+ 2 x yOt'=180 ( vì xOt=tOy;yOt'=t'Ox')
2x(tOy+yOt')=180
tOy+yOt'=180:2=90
tOt'=90

Giải:
Vì \(x\widehat{O}y\) và \(y\widehat{O}x'\) là 2 góc kề bù
\(\Rightarrow x\widehat{O}y+y\widehat{O}x'=180^o\)
\(70^o+y\widehat{O}x'=180^o\)
\(y\widehat{O}x'=180^o-70^o\)
\(y\widehat{O}x'=110^o\)
Vì Ot là tia p/g của \(x\widehat{O}y\)
\(\Rightarrow x\widehat{O}t=t\widehat{O}y=\dfrac{x\widehat{O}y}{2}=\dfrac{70^o}{2}=35^o\)
Vì Ot' là tia p/g của \(y\widehat{O}x'\)
\(\Rightarrow y\widehat{O}t'=t'\widehat{O}x'=\dfrac{y\widehat{O}x'}{2}=\dfrac{110^o}{2}=55^o\)
\(\Rightarrow t\widehat{O}y+y\widehat{O}t'=t\widehat{O}t'\)
\(35^o+55^o=t\widehat{O}t'\)
\(\Rightarrow t\widehat{O}t'=90^o\)
\(\Rightarrow x\widehat{O}y+y\widehat{O}t'=x\widehat{O}t'\)
\(70^o+55^o=x\widehat{O}t'\)
\(\Rightarrow x\widehat{O}t'=125^o\)
Chúc bạn học tốt!
180 độ