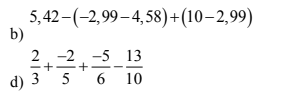Giải hộ em với ạ mn ơi!

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



TK :
- Cạnh huyền góc nhọn: Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn tương ứng của tam giác vuông kia thì 2 tam giác đó bằng nhau.
- Cạnh góc vuông-góc nhọn kề: Nếu cạnh huyền và góc nhọn kề của tam giác vuông này bằng cạnh huyền và góc nhọn kề tương ứng của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

\(a^2x+a^2y+ax+ay+x+y\)
\(=a^2\left(x+y\right)+a\cdot\left(x+y\right)+\left(x+y\right)\)
\(=\left(x+y\right)\cdot\left(a^2+a+1\right)\)

428=22.107
422=2.211
115=5.23
180=22.32.5
160=25.5
190=2.5.9
250=2.53
350=2.52.7
324=22.34
364=22.7.13
270=2.33.5
290=2.5.29
120=23.3.5
150=2.3.52
160=25.5
\(428=2^2\cdot107\)
\(422=2\cdot211\)
\(115=5\cdot23\)
\(180=2^2\cdot3^2\cdot5\)
\(160=2^5\cdot5\)
\(190=2\cdot5\cdot19\)
\(250=2\cdot5^3\)
\(350=2\cdot5^2\cdot7\)
\(324=2^2\cdot3^4\)
\(364=2^2\cdot7\cdot13\)
\(270=3^3\cdot2\cdot5\)
\(290=2\cdot5\cdot29\)
\(120=2^3\cdot3\cdot5\)
\(150=5^2\cdot2\cdot3\)
\(160=2^5\cdot5\)

SP= là điểm bạn đc bọn mik k (lưu ý phải là người trên 10SP)
GP là điểm bạn đc giáo viên k


\(b,B=\dfrac{x-4+2\sqrt{x}+6-3\sqrt{x}-4}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\\ B=\dfrac{x-\sqrt{x}+2}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\\ c,M=B:A=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\cdot\dfrac{\sqrt{x}+3}{x-\sqrt{x}+2}=\dfrac{\sqrt{x}+1}{x-\sqrt{x}+2}\\ M=\dfrac{x-\sqrt{x}+2-x+2\sqrt{x}-1}{x-\sqrt{x}+2}\\ M=1-\dfrac{x-2\sqrt{x}+1}{x-\sqrt{x}+2}=1-\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\)
Ta có \(\left(\sqrt{x}-1\right)^2\ge0;x-\sqrt{x}+2=\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{7}{4}>0\)
Do đó \(\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\ge0\)
\(\Leftrightarrow M=1-\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\le1-0=1\)
Vậy \(M_{max}=1\Leftrightarrow\sqrt{x}=1\Leftrightarrow x=1\left(tm\right)\)
a: Thay \(x=3+2\sqrt{2}\) vào A, ta được:
\(A=\dfrac{3+2\sqrt{2}-\sqrt{2}-1+2}{\sqrt{2}+1+3}=\dfrac{4+\sqrt{2}}{4+\sqrt{2}}=1\)
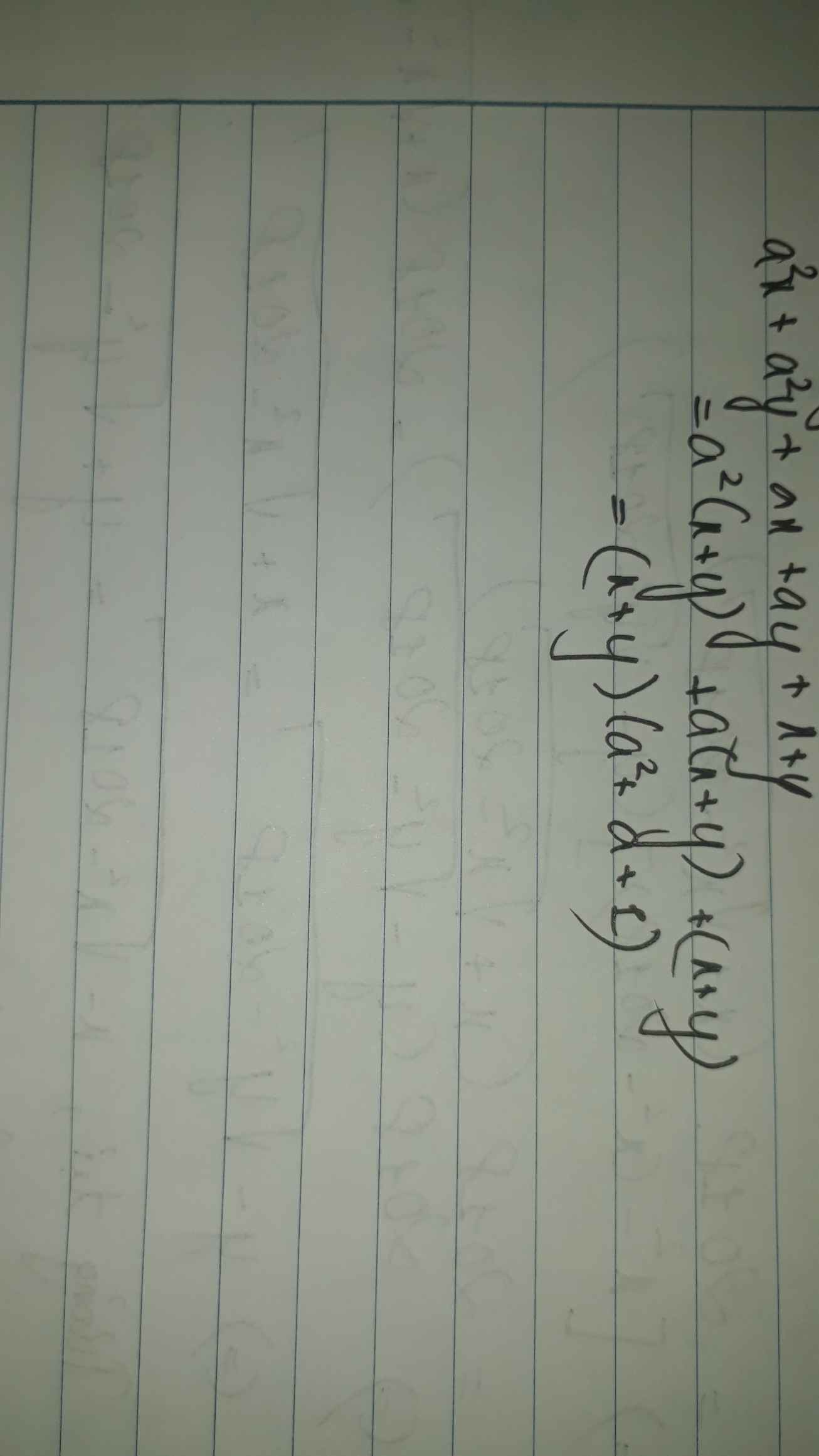
 Mn ơi, giải hộ mik câu này với! Tối nay mik phải nộp rồi ạ! Cảm ơn mn nhiều lắm!
Mn ơi, giải hộ mik câu này với! Tối nay mik phải nộp rồi ạ! Cảm ơn mn nhiều lắm!