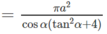Một chiếc kệ sách để bàn gồm các giá đỡ là 9 hình tam giác đều bằng nhau như hình bên. Biết cạnh của tam giác đều là 18cm và khoảng cách giữa mỗi tam giác đều là 2cm. Em hãy tính tiền nguyên liệu phải trả khi thiết kế chiếc giá đỡ trên.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
SN
25 tháng 9 2021
.
SBMNP=450√3cm2SBMNP=4503cm2.
Giải thích các bước giải:
Tam giác ABC có chu vi 180cm nên AB=1803=60cmAB=1803=60cm.
Do BMNP là hình thoi
⇒MN∥BP⇒MN∥BC⇒MN∥BP⇒MN∥BC.
Áp dụng định lí Ta-lét ta có:
MNBC=AMAB=BMBCMNBC=AMAB=BMBC.
Mà AM=BMAM=BM suy ra M là trung điểm của AB.
CMTT ta có N là trung điểm của AC và P là trung điểm của BC.
MP là đường trung bình của tam giác ABC.
⇒MP=12AC=12.60=30(cm)⇒MP=12AC=12.60=30(cm).
N là trung điểm của AC nên AN=12.60=30(cm)AN=12.60=30(cm).
Áp dụng định lí Pytago trong tam giác vuông ABN có:
BN=√AB2−AN2BN=√602−302BN=30√3(cm)BN=AB2−AN2BN=602−302BN=303(cm)
Vậy SBMNP=12BN.MP=12.30√3.30=450√3(cm2)
CM
21 tháng 1 2018
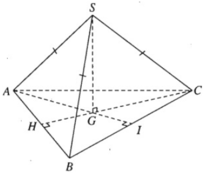
a) SG là trục đường tròn ngoại tiếp tam giác đều ABC nên SG ⊥ (ABC). Ta có
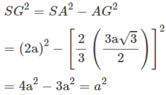
Vậy khoảng cách từ S tới mặt phẳng (ABC) là độ dài của đoạn SG = a
Ta có CG ⊥ AB tại H. Vì GH là đoạn vuông góc chung của AB và SG, do đó
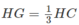
mà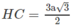 
nên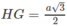 
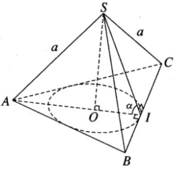
CM
14 tháng 12 2019
Gọi I là trung điểm của cạnh BC và O là tâm của tam giác đều ABC. Theo giả thiết ta có SA = SB = SC = a và ∠ SIO = α. Đặt OI = r, SO = h, ta có AO = 2r và
Do đó a 2 = r 2 tan 2 α + 4 r 2 = r 2 tan 2 α + 4
Vậy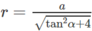 
Hình nón nội tiếp có đường sinh là :
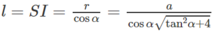
Diện tích xung quanh của hình nón nội tiếp hình chóp S.ABC là:
