Nếu một số có 2 chữ số mà hiệu giữa bình phương của số đó với bình phương tổng các chữ số của nó là 99 thì số cần tìm là số nào
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
28 tháng 5 2019
Gọi a là chữ số hàng chục, b là chữ số hàng đơn vị. Điều kiện a, b nguyên 1 ≤ a ≤ 9 và 0 ≤ b ≤ 9. Ta có:
'
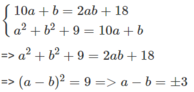Trường hợp 1
a - b = 3 ⇒ a = b + 3
Thay vào phương trình đầu của hệ phương trình ta được:
11b + 30 = 2(b + 3)b + 18 ⇒ 2 b 2 - 5 b + 12 = 0
Phương trình cuối có hai nghiệm: b 1 = 4 , b 2 = -3/2
Giá trị b 2 = -3/2 không thỏa mãn điều kiện 0 ≤ b ≤ 9 nên nên bị loại.
Vậy b = 4, suy ra a = 7.
Trường hợp 2
a - b = - 3 ⇒ a = b - 3
Thay vào phương trình của hệ phương trình ra được
11b - 30 = 2(b - 3)b + 18 ⇒ 2 b 2 - 17 b + 48 = 0
Phương trình này vô nghiệm.
Vậy số phải tìm là 74.
BT
5 tháng 5 2017
Gọi số cần tìm có dạng: \(\overline{ab}\) \(\left(a,b\in N;a,b>0\right)\)
Thương của số cần tìm với tích hai chữ số của nó có dạng:\(\overline{ab}:\left(ab\right)\).
Theo giả thiết ta có: \(\overline{ab}=2ab+18\).
Tổng bình phương các chữ số của số cần tìm là: \(a^2+b^2+9=\overline{ab}\).
Ta có hệ phương trình: \(\left\{{}\begin{matrix}2ab+18=\overline{ab}\\a^2+b^2+9=\overline{ab}\end{matrix}\right.\)\(\Rightarrow a^2+b^2+9=2ab+18\)\(\Leftrightarrow\left(a-b\right)^2=9\)\(\Leftrightarrow\left|a-b\right|=3\).
Th 1. \(a-b=3\)\(\Leftrightarrow a=b+3\). Khi đó:
\(2ab+18=\overline{ab}\)\(\Leftrightarrow2ab+18=10a+b\)\(\Leftrightarrow2\left(b+3\right)b+18=10\left(b+3\right)+b\)\(\Leftrightarrow2b^2-5b-12=0\)\(\Leftrightarrow\left\{{}\begin{matrix}b=4\left(tm\right)\\b=\dfrac{-3}{2}\left(l\right)\end{matrix}\right.\).
Với \(b=4\) ta có \(a=3+b=3+4=7\). Vậy số đó là 73.
Th2: \(a-b=-3\)\(\Leftrightarrow a=b-3\). Khi đó:
\(2ab+18=10a+b\)\(\Leftrightarrow2\left(b-3\right)b+18=10\left(b-3\right)+b\)
\(\Leftrightarrow2b^2-17b+48=0\) (Vô nghiệm).
Vậy số cần tìm là: 73.
28 tháng 6 2015
Gọi số cần tìm là ab.
Ta có (ab)2 = a3 + b3
Giả sử ab = 33 = 9
thì (ab)2 = 81 => a3 + b3 = 81. Bạn tìm chữ số a và b => điều phải chứng minh
TM
5
24 tháng 10 2017
(ab)^2=(a+b)^3
Từ đó suy ra (ab) phải là lập phương của 1 số, a+b là bình phương của 1 số
(ab) = 27 hoặc 64
chỉ có 27 thỏa mãn
vậy (ab)=27
DT
0
NH
0
HA
1
25 tháng 11 2016
Gỉa sử x và y là 2 số phải tìm và x^2 = y^3 = a. Phân tích a ra thừa số nguyên tố , ta thấy các số mũ của các thừa số nguyên tố phải chia hết cho 2 vì a = x^2 , lại phải chia hết cho 3 vì a= y^3 . Khi đó , a là lũy thừa bấc 6 của 1 số tự nhiên nào đó . Vì a lớn hơn hoặc = 100 và nhỏ hơn 10000 nên a có thể = 3^6 hoặc 4^ 6 . Nhưng 3^6= ( 3^2 )^3 ko phải là lập phương của 1 số có 2 chữ số còn 4^6 = (2^2)^6 =( 2^ 6) ^2 = 64^2 và 4^6 = 2^ 12 = ( 2^4 ) ^3 = 16^3 . Vậy 2 số phải tìm là 64 và 16.
PT
1
CM
17 tháng 8 2018
Gọi số cần tìm là a b a , b ∈ N ; 1 ≤ a ≤ 9 ; b ≤ 9
Từ đầu bài: đặt: a b = x 3 ; a + b = x 2 x ∈ N
Vì : 10 < a b < 100 nên 10 ≤ x 3 ≤ 100 ta có 2 3 < x 3 < 5 3
Suy ra: 2 < x < 5 => x ∈ {3;4}
* Với: x = 3 => a b = 3 3 = 27
a = 2; b = 1 thỏa mãn a b 2 = a + b 3 . Vì: 27 2 = ( 2 + 7 ) 3 = 729
* Với: x = 4 => a b = 4 3 = 64
a = 6; b = 4 không thỏa mãn a b 2 = a + b 3 . Vì 64 2 ≠ ( 6 + 4 ) 3
Vậy số cần tìm là 27
PT
1
Gọi số đó là: ab
Theo đề bài: (ab)2 - (a+ b)2 = 99
=> (10a + b)2 - (a + b)2 = 99
=> (10a + b). (10a + b) - (a+ b).(a+b) = 99
=>...
=> 99a2 + 18ab = 99 => 9a.(11a + b) = 99 => a.(11a + b) = 11 = 1.11
=> a = 1; 11a + b = 11
=> a = 1; b = 0
Vậy số đó là 10
+) Nếu đề bài bò đi "bình phương " ở tổng các chữ số :
Ta có: (ab)2 - a - b = 99 => ab2 = 99 + a + b
Vì a; b là các chữ số nên a + b < 20 => ab2 < 99 + 20 = 119
Mà ab2 là bình phương của số có 2 chữ số nên ab2 = 100 = 102
Vậy số đó là 10
+) bạn chú ý: Viết đề rõ ràng.