Cho góc xAy nhỏ hơn 90 độ có tia phân giác At, trên tia At lấy điểm O(O khác A), Một đường thẳng qua O cắt Ax, Ay lần lượt tại E và F(E và F khác A). Xác định vị trí của E và F để diện tích tam giác AEF bé nhất.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
30 tháng 4 2017
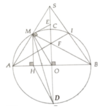
a, Chứng minh ∆MEF:∆MOA
b, ∆MEF:∆MOA mà AO=OM => ME=EF
c, Chứng minh F là trực tâm của ∆SAB, AI là đường cao, chứng minh A,I,F thẳng hàng
d, FA.SM = 2 R 2
e, S M H O = 1 2 OH.MH ≤ 1 2 . 1 2 M O 2 = 1 4 R 2
=> M ở chính giữa cung AC
18 tháng 1 2018
Trường hợp 1: Đường thẳng d song song với BC.
Theo định lý Ta - lét ta có:\(\frac{BE}{EA}=\frac{OD}{OA}\frac{CD}{FA}=\frac{OD}{OA}\)
Suy ra : \(\frac{BE}{AE}+\frac{CF}{AF}=1\Leftrightarrow\frac{OD}{OA}+\frac{OD}{OA}=1\Leftrightarrow2OD=OA\left(1\right)\)
TRƯỜNG HỢP 2 LÀM TƯƠNG TỰ NHA :D
3 tháng 2 2017
Kẻ \(AA';BB';CC'⊥d\); ta có AA' // BB' // CC'.
Có AA' // BB' \(\Rightarrow\frac{BE}{AE}=\frac{BB'}{AA'}\)( Định lý Ta-lét )
Tương tự; lại có \(\frac{CF}{AF}=\frac{CC'}{AA'}\)
\(\Rightarrow\frac{BE}{AE}+\frac{CF}{AF}=\frac{BB'}{AA'}+\frac{CC'}{AA'}=1\)
\(\Rightarrow\frac{BB'+CC'}{AA'}=1\)
\(\Rightarrow AA'=BB'+CC'\)
Xét hình thang BB'C'C có DD' // BB' // CC' và D là trung điểm BC nên DD' là đường trung bình hình thang.
\(\Rightarrow DD'=\frac{BB'+CC'}{2}=\frac{AA'}{2}\)
\(\Rightarrow\frac{AA'}{DD'}=2\)
Có AA' // DD' nên \(\frac{AA'}{DD'}=\frac{AO}{OD}=2\)
Suy ra O là trọng tâm tam giác ABC.
Vậy ...
