Cho hình thang cân ABCD có đường chéo BD vuông góc với cạnh bên BC. DB là tia phân giác của góc D. Biết BC = 3cm, chu vi của hình thang là …cm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 9 2016
hình thang ABCD
=> AD=BC = 3cm ( định lí 1 )
AB//CD ( ABCD là hình thang cân )
=> góc B1 = góc D2 ( SLT )
góc D1 = góc D2 ( gt )
=> góc B1 = góc D1
=> tg ABD cân tại A
=> AD=AB= 3cm
tg DBC vuông ở B
hình thang cân ABCD
=> góc D = góc C
2 lần góc D1 = góc C
=> góc DBC = góc D1 + 2 lần góc D1 = 90 độ
3 lần góc D1 = 90 độ
=> góc D1 = 900 : 3
= 300
=> góc C = 900 - góc D1 = 900 - 300 = 600
Gọi DA giao CB tại O
tg ODC có DB là pgiác
BD vuông góc với Oc
=> tg ODC cân ở D
lại có góc C = 60 độ
=> tg OCD đều
=> CD = CO
mà tg ODC đều nên DB là đường phân giác đồng thời là đường trung tuyến
=> OB= BC
CD= CO = OB+BC
mà OB = BC ( cmt )
=> CĐ= CƠ = 2CB = 2.3 = 6 ( cm )
Chu vi của hình thang cân ABCD là
AB+BC+AD+CD = 3+3+3+6= 15 (cm )
11 tháng 10 2021
hình thang ABCD
=> AD=BC = 3cm ( định lí 1 )
AB//CD ( ABCD là hình thang cân )
=> góc B1 = góc D2 ( SLT )
góc D1 = góc D2 ( gt )
=> góc B1 = góc D1
=> tg ABD cân tại A
=> AD=AB= 3cm
tg DBC vuông ở B
hình thang cân ABCD
=> góc D = góc C
2 lần góc D1 = góc C
=> góc DBC = góc D1 + 2 lần góc D1 = 90 độ
3 lần góc D1 = 90 độ
=> góc D1 = 900 : 3
= 300
=> góc C = 900 - góc D1 = 900 - 300 = 600
Gọi DA giao CB tại O
tg ODC có DB là pgiác
BD vuông góc với Oc
=> tg ODC cân ở D
lại có góc C = 60 độ
=> tg OCD đều
=> CD = CO
mà tg ODC đều nên DB là đường phân giác đồng thời là đường trung tuyến
=> OB= BC
CD= CO = OB+BC
mà OB = BC ( cmt )
=> CĐ= CƠ = 2CB = 2.3 = 6 ( cm )
Chu vi của hình thang cân ABCD là
AB+BC+AD+CD = 3+3+3+6= 15 (cm )
CM
17 tháng 6 2019
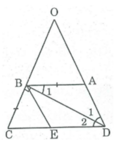
Ta có: AD = BC = 3 (cm) (tính chất hình thang cân)
∠ (ABD) = ∠ (BDC) (so le trong)
∠ (ADB) = ∠ (BDC) ( do DB là tia phân giác của góc D )
⇒ ∠ (ABD) = ∠ (ADB)
⇒ ∆ ABD cân tại A
⇒ AB = AD = 3 (cm)
∆ BDC vuông tại B
∠ (BDC) + ∠ C = 90 0
∠ (ADC) = ∠ C (gt)
Mà ∠ (BDC) = 1/2 ∠ (ADC) nên ∠ (BDC) = 1/2 ∠ C
∠ C + 1/2 ∠ C = 90 0 ⇒ ∠ C = 60 0
Từ B kẻ đường thẳng song song AD cắt CD tại E.
Hình thang ABED có hai cạnh bên song song nên AB = DE và AD = BE
⇒ DE = 3 (cm), BE = 3 (cm)
∠ (BEC) = ∠ (ADC) (đồng vị)
Suy ra: ∠ (BEC) = ∠ C
⇒ ∆ BEC cân tại B có ∠ C = 60 0
⇒ ∆ BEC đều
⇒ EC = BC = 3 (cm)
CD = CE + ED = 3 + 3 = 6(cm)
Chu vi hình thang ABCD bằng:
AB + BC + CD + DA = 3 + 3 + 6 + 3 = 15 (cm)
