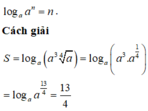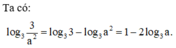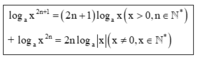cho 3 số thực bất kì x:y;z thỏa mãn x^2010+y^2010+z^2010=3 tìm giá trị lớn nhất của x^2+y^2+z^2 ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{a^2+b^2+c^2}{3}\ge\left(\dfrac{a+b+c}{3}\right)^2\)
\(\Leftrightarrow\dfrac{a^2+b^2+c^2}{3}\ge\dfrac{\left(a+b+c\right)^2}{9}\)
\(\Leftrightarrow3\left(a^2+b^2+c^2\right)\ge\left(a+b+c\right)^2\)
\(\Leftrightarrow3\left(a^2+b^2+c^2\right)\ge a^2+b^2+c^2+2\left(ab+bc+ac\right)\)
\(\Leftrightarrow2a^2+2b^2+2c^2-2\left(ab+bc+ac\right)\ge0\)
\(\Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\)(đúng)
Dấu "=" xảy ra \(\Leftrightarrow a=b=c\)

Vì tổng 7 số bất kì là số thực dương nên trong 2017 số đã cho tồn tại 1 số thực dương
Tách riêng số thực dương đó ra ta còn 2016 sô
Chia 2016 số thành 288 nhóm , mỗi nhóm có 7 số
MÀ tổng 7 số bất kì là số thực dương nên mỗi nhóm trong số 288 nhóm đều dương
=> Tổng của 288 nhóm đều dương
Cộng thêm số dương lúc đầu tách được tổng của 2017 số ấy đều dương (Đpcm)

Chọn đáp án C
Phương pháp
Sử dụng các công thức lũy thừa thu gọn biểu thức dưới dấu logarit và sử dụng công thức