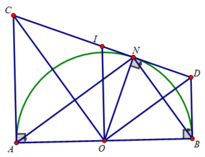
cho AB=18 cm. C\(\in\)AB: AC=6 cm
trên cùng một nửa mặt phẳng bờ AB vẽ nửa đường tròn \(\left(O_1;\frac{AC}{2}\right)\)và nửa đường tròn \(\left(O_2;\frac{BC}{2}\right)\). Vẽ tiếp tuyến chung ngoài MK (\(\left(M\in\left(O_1\right)\right)\);\(\left(K\in\left(O_2\right)\right)\) ) AM cắt BK ở I; MK cắt đường tròn \(\left(O;\frac{AB}{2}\right)\)ở E;D. Chứng minh:
a)\(CI⊥AB\)
b)Tính ED