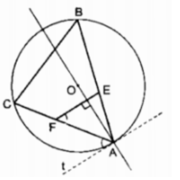
Cho đường tròn (o) có hai đường kính AC và BD vuông góc với nhau. Một điểm M bất kì trên cung nhỏ AB (M không trùng với A), đường thẳng MD cắt AC tại E và cắt đường thẳng BC tại F.
1. Chứng minh bốn điểm : B,M,E,O cùng thuộc một đường tròn
2. Chứng minh EF.MD= AD.FC
3. Điểm M ở vị trí nào trên cung AB thì tâm đường tròn ngoại tiếp △AME gần tâm O nhất
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, HS tự chứng minh
b, Chứng minh ∆NMC:∆NDA và ∆NME:∆NHA
c, Chứng minh ∆ANB có E là trực tâm => AE ⊥ BN mà có AK ⊥ BN nên có ĐPCM
Chứng minh tứ giác EKBH nội tiếp, từ đó có A K F ^ = A B M ^
d, Lấy P và G lần lượt là trung điểm của AC và OP
Chứng minh I thuộc đường tròn (G, GA)


Vì tổng các góc trong tứ giác bằng \(360^0\) mà \(\widehat{CBE}+\widehat{EFC}=180^0\) nên suy ra \(\widehat{BCF}+\widehat{BEF}=180^0\)

Gọi IE,IF cắt đường tròn (O) lần thứ hai lần lượt tại H,K. Lúc đó ta có ^BIH = ^CIK = 900
=> ^BIH và ^CIK chắn nửa đường tròn (O) => BH,CK là các đường kính của (O)
Xét bộ 6 điểm A,B,C,H,I,K cùng nằm trên (O): BH cắt CK tại O, IH cắt AC tại E, IK cắt AB tại F
Suy ra 3 điểm E,O,F thẳng hàng (ĐL Pascal). Hay EF đi qua O cố định (đpcm).
P/S: Định lí Pascal khá nổi tiếng, bạn có thể tham khảo cách chứng minh trong các sách nâng cao (NC&PT Toán 9 tập 2).