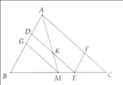
Cho tam giác ABC, trung tuyến Am, điểm D thuộc AC. Gọi I là giao điểm của AM và BD. Qua C kẻ đường thẳng song song với AB cắt BD ở K. CM: IB2=ID.IK
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 3 2018
P/s hình tự vẽ lấy :)
Ta có: AM cắt CK tại E
Xét tam giác AMB và tam giác EMC có:
\(MB=MC\left(gt\right)\)
\(\widehat{AMB}=\widehat{CME}\)( đối đỉnh )
\(\widehat{ABM}=\widehat{ECM}\)( so le trong và AB // CE )
\(\Rightarrow\Delta AMB=\Delta EMC\left(g-c-g\right)\)
\(\Rightarrow MA=ME\)( hai cạnh tương ứng )
Và BM = MC ( Vì M là trung tuyến AM )
Suy ra ABCE là hình bình hành
\(\Rightarrow BE//AC\Rightarrow\frac{IB}{ID}=\frac{IA}{IE}\left(1\right)\)
\(\Rightarrow\frac{IB}{IK}=\frac{IA}{IE}\left(2\right)\)
Từ ( 1 ) và ( 2 ) suy ra \(\frac{ID}{IB}=\frac{IB}{IK}\)
\(\Rightarrow IB^2=ID.IK\left(đpcm\right)\)
Vậy \(IB^2=ID.IK\)
TM
23 tháng 2 2023
a.Xét ΔDAB,ΔDMBΔ���,Δ��� có:
ˆDAB=ˆDMB(=90o)���^=���^(=90�)
Chung BD��
ˆABD=ˆMBD���^=���^
→ΔDAB=ΔDMB→Δ���=Δ���(cạnh huyền-góc nhọn)
b.Từ câu a →BA=BM,DA=DM→��=��,��=��
→B,D∈→�,�∈ trung trực AM��
→DB→�� là trung trực AM��
c.Ta có: DM⊥BC→KD⊥BC��⊥��→��⊥��
CA⊥AB→CD⊥BK��⊥��→��⊥��
→D→� là trực tâm ΔBCKΔ���
→BD⊥CK→��⊥��
→BN⊥KC→��⊥��
Xét ΔBMK,ΔBACΔ���,Δ��� có:
Chung ^B�^
BM=BA��=��
ˆBMK=ˆBAC(=90o)���^=���^(=90�)
→ΔBMK=ΔBAC(c.g.c)→Δ���=Δ���(�.�.�)
→BK=BC→��=��
→ΔKBC→Δ��� cân tại B�
d.Ta có: ΔBCKΔ��� cân tại B,BN⊥CK→N�,��⊥��→� là trung điểm KC��
Trên tia đối của tia NP�� lấy điểm F� sao cho NP=NF��=��
Xét ΔNKP,ΔNCFΔ���,Δ��� có:
NK=NC��=��
ˆKNP=ˆCNF���^=���^
NP=NF��=��
→ΔNKP=ΔNCF(c.g.c)→Δ���=Δ���(�.�.�)
→KP=CF,ˆNKP=ˆNCF→KP//CF→CF//BP→��=��,���^=���^→��//��→��//��
Xét ΔFPC,ΔBPCΔ���,Δ��� có:
ˆCPF=ˆPCB���^=���^ vì NP//BC��//��
Chung NP��
ˆPCF=ˆCPB���^=���^ vì BP//CF��//��
→ΔFPC=ΔBCP(g.c.g)→Δ���=Δ���(�.�.�)
→CF=BP→��=��
→PK=BP→��=��
→P→� là trung điểm BK��
Do E,N�,� là trung điểm BC,CK��,��
→KE,BN,CP→��,��,�� đồng quy tại trọng tâm ΔKBCΔ���
