Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
Gọi vận tốc cano là x
Vận tốc cano khi đi là x+3
Vận tốc cano khi về là x-3
Theo đề, ta có: 15/x+3+15/x-3=3-1/3=8/3
=>(15x-45+15x+45)/(x^2-9)=8/3
=>8x^2-72=3*30x=90x
=>8x^2-90x-72=0
=>x=12
1:
Gọi vận tốc cano là x
=>Vận tốc lúc đi là x+4, vận tốc lúc về là x-4
Theo đề, ta co: 30/x-4-30/x+4=1
=>(30x+120-30x+120)/(x^2-16)=1
=>x^2-16=240
=>x^2=256
=>x=16

gọi x (Km/ h)là vận tốc của ca nô khi nước yên lặng
vận tốc khi đi suôi dòng là x + 3
vận tốc khi đi ngực dòng là x - 3
thời gian khi đi suôi dòng là \(\dfrac{30}{x+3}\)
thời gian khi đi ngực dòng là \(\dfrac{30}{x-3}\)
thời gian nghỉ là 40 phút = \(\dfrac{40}{60}\) = \(\dfrac{2}{3}\) giờ
vì tổng thời gian từ lúc đi đến lúc trở về là 6 giờ
nên ta có phương trình :
\(\dfrac{30}{x+3}\)+\(\dfrac{30}{x-3}\)+\(\dfrac{2}{3}\) = 6
\(\Leftrightarrow\) \(\dfrac{30.\left(x-3\right)+30.\left(x+3\right)}{\left(x+3\right)\left(x-3\right)}\) +\(\dfrac{2}{3}\) = 6
\(\Leftrightarrow\) \(\dfrac{60x}{x^2-9}\)+\(\dfrac{2}{3}\) = 6\(\Leftrightarrow\) \(\dfrac{60x}{x^2-9}\)= \(\dfrac{16}{3}\)
\(\Leftrightarrow\) 180x = 16x2 - 144\(\Leftrightarrow\) 16x2 -180x -144 = 0
\(\Leftrightarrow\) 4x2 - 45x -36 = 0
giải \(\Delta\) ta có 2 nghiệm :x1=12 (tmđk) ; x2=-\(\dfrac{3}{4}\) (loại)
vậy vận tốc khi nước yên lặng là 12(Km/h)

Gọi x (km/h) là vận tốc của ca nô khi nước yên lặng.
Điều kiện: x > 3
Khi đó vận tốc khi đi xuôi dòng trên sông là x + 3 (km/h)
vận tốc khi đi ngược dòng trên sông là x – 3 (km/h)
thời gian ca nô đi xuôi dòng là 30/(x + 3) (giờ)
thời gian ca nô đi ngược dòng là 30/(x - 3) (giờ)
thời gian ca nô nghỉ ở B là 40 phút = 2/3 (giờ)
Theo đề bài, ta có phương trình:
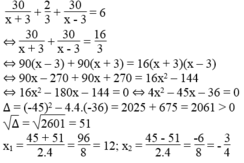
Giá trị x = - 3/4 không thỏa mãn điều kiện bài toán.
Vậy vận tốc của ca nô khi nước yên lặng là 12 km/h.

Gọi vận tốc thực tế của ca nô là x ( km/h ) ( x > 0 )
Vận tốc của ca nô khi xuôi dòng là: \(x+4\)( km/h ) ( lấy vận tốc ca nô + với vận tốc nước )
Thời gian xuôi dòng của ca nô là: \(\frac{30}{x+4}\)( giờ )
Vận tốc ngược dòng của ca nô là: \(x-4\)( km/h ) ( lấy vận tốc ca nô - với vận tốc nước )
Thời gian ngược dòng của ca nô là: \(\frac{30}{x-4}\)( giờ )
Theo đề bài ta có phương trình:
\(\frac{30}{x+4}+\frac{30}{x-4}=4\)
Giải nốt cái phương trình rồi kết luận
Toán lớp 5 kì 2 , ko phải toán lớp 9 => bịa là toán 9 => ko làm

Gọi vận tốc cano khi mặt nước yên lặng là x (km/h) (x>3)
Ta có : Vận tốc cano khi xuôi dòng là : x + 3 (km/h)
Vận tốc cano khi ngược dòng là : x - 3 (km/h)
Phương trình : \(\frac{15}{x+3}+\frac{20}{60}+\frac{15}{x-3}=3\)
\(\Leftrightarrow\frac{1}{x+3}+\frac{1}{x-3}=\frac{8}{45}\)
Giải phương trình trên ta được x = 12 (vì x>0)
Vậy : Vận tốc cano khi nước yên lặng là 12 km/h

Gọi vận tốc của ca nô khi nước yên lặng là x(km/h; x>4)
=> Vận tốc xuôi dòng của ca nô là x+4(km/h)
Vận tốc ngược dòng của ca nô là x-4(km/h)
Theo bải ra:
Khoảng cách giữa 2 bến sông A và B là 48 km
=> Thời gian xuôi dòng của ca nô:\(\frac{48}{x+4}\)(h)
Thời gian ngược dòng của ca nô:\(\frac{48}{x-4}\)(h)
Cả thời gian đi và về là 5(h)
=>\(\frac{48}{x+4}+\frac{48}{x-4}=5\)
=>\(\frac{48\left(x-4\right)}{\left(x+4\right)\left(x-4\right)}+\frac{48\left(x+4\right)}{\left(x+4\right)\left(x-4\right)}=\frac{5\left(x+4\right)\left(x-4\right)}{\left(x+4\right)\left(x-4\right)}\)
=>\(48\left(x-4\right)+48\left(x+4\right)=5\left(x+4\right)\left(x-4\right)\)
=>\(48x-192+48x+192=\left(5x+20\right)\left(x-4\right)\)
=>\(96x=5x^2-80\)
=>\(5x^2-96x-80=0\)
=>\(\orbr{\begin{cases}x=20\left(TM\right)\\x=\frac{-4}{5}\left(KTM\right)\end{cases}}\)
Vậy vận tốc của ca nô khi nước yên lặng là 20 km/h